
【题目】【2017山西孝义考前热身】已知函数![]() (
(![]() 是常数),
是常数),
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,函数
时,函数![]() 有零点,求
有零点,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(Ⅱ)![]() 或
或![]() .
.
【解析】试题分析:
(1)首先求解导函数,然后结合参数的范围分类讨论即可得到函数的单调区间;
(2)结合(1)的结论讨论函数的最值,结合题意得到关于实数a的不等式,求解不等式可得![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.
试题解析:
(1) 根据题意可得,当![]() 时,
时, ![]() ,函数在
,函数在![]() 上是单调递增的,在
上是单调递增的,在![]() 上是单调递减的,
上是单调递减的,
当![]() 时,
时, ![]() ,因为
,因为![]() ,
,
令![]() ,解得
,解得![]() 或
或![]()
①当![]() 时,函数
时,函数![]() 在
在![]() ,
, ![]() 上有
上有![]() ,即
,即![]() ,函数
,函数![]() 单调递减;函数
单调递减;函数![]() 在
在![]() 上有
上有![]() ,即
,即![]() ,函数
,函数![]() 单调递增;
单调递增;
②当![]() 时,函数
时,函数![]() 在
在![]() 上有
上有![]() ,即
,即![]() ,函数
,函数![]() 单调递增;函数
单调递增;函数![]() 在
在![]() 上有
上有![]() ,即
,即![]() ,函数
,函数![]() 单调递减;
单调递减;
综上所述,当![]() 时,函数
时,函数![]() 的单调递增区间
的单调递增区间![]() ,递减区间为
,递减区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的单调递减区间为
的单调递减区间为![]() ,递增区间为
,递增区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,递减区间为
,递减区间为![]() ;
;
(1)①当![]() 时,
时, ![]() 可得
可得![]() ,故
,故![]() 可以;
可以;
②当![]() 时,函数
时,函数![]() 的单调递减区间为
的单调递减区间为![]() ,递增区间为
,递增区间为![]() ,
,
(Ⅰ) 若![]() ,解得
,解得![]() ;
;
可知: ![]() 时,
时, ![]() 是增函数,
是增函数, ![]() 时,
时, ![]() 是减函数,
是减函数,
由![]() 在
在![]() 上
上![]() ;
;
解得![]() ,所以
,所以![]() ;
;
(Ⅱ)若![]() ,解得
,解得![]() ;
;
函数![]() 在
在![]() 上递增,
上递增,
由![]() ,则
,则![]() ,解得
,解得![]()
由![]() ,即此时无解,所以
,即此时无解,所以![]() ;
;
③当![]() 时,函数
时,函数![]() 在
在![]() 上递增,类似上面
上递增,类似上面![]() 时,此时无解,
时,此时无解,
综上所述, ![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)的导函数f'(x)满足2f(x)+xf′(x)>x2(x∈R),则对x∈R都有( )
A.x2f(x)≥0
B.x2f(x)≤0
C.x2[f(x)﹣1]≥0
D.x2[f(x)﹣1]≤0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ ![]() ax2+x,a∈R.
ax2+x,a∈R.
(1)若f(1)=0,求函数f(x)的最大值;
(2)令g(x)=f(x)﹣(ax﹣1),求函数g(x)的单调区间;
(3)若a=﹣2,正实数x1 , x2满足f(x1)+f(x2)+x1x2=0,证明x1+x2≥ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017广东佛山二模】某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为![]() 、
、![]() 、
、![]() 三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).


(Ⅰ)根据规定,该产品各工种保单的期望利润都不得超过保费的20%,试分别确定各类工种每张保单保费的上限;
(Ⅱ)某企业共有职工20000人,从事三类工种的人数分布比例如图,老板准备为全体职工每人购买一份此种保险,并以(Ⅰ)中计算的各类保险上限购买,试估计保险公司在这宗交易中的期望利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017四川资阳4月模拟】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100] 分成5组,制成如图所示频率分直方图.
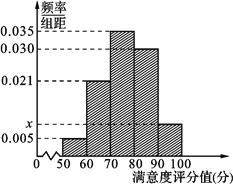
(Ⅰ) 求图中![]() 的值;
的值;
(Ⅱ) 已知满意度评分值在[90,100]内的男生数与女生数的比为2:1,若在满意度评分值为[90,100]的人中随机抽取4人进行座谈,设其中的女生人数为随机变量X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上![]() 件产品作为样本称出它们的重量(单位:克),重量的分组区间为
件产品作为样本称出它们的重量(单位:克),重量的分组区间为![]() ,
,![]() , ,
, ,![]() ,由此得到样本的频率分布直方图,如图所示.
,由此得到样本的频率分布直方图,如图所示.
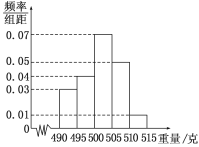
(1)根据频率分布直方图,求重量超过![]() 克的产品数量;
克的产品数量;
(2)在上述抽取的![]() 件产品中任取
件产品中任取![]() 件,设
件,设![]() 为重量超过
为重量超过![]() 克的产品数量,求
克的产品数量,求![]() 的分布列;
的分布列;
(3)从该流水线上任取![]() 件产品,求恰有
件产品,求恰有![]() 件产品的重量超过
件产品的重量超过![]() 克的概率.
克的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同, 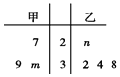
(1)求m,n的取值.
(2)比较甲、乙两组数据的稳定性,并说明理由.
注:方差公式s2= ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com