
【题目】设函数f(x)=ax2+(b﹣8)x﹣a﹣ab的两个零点分别是﹣3和2.
(Ⅰ)求f(x);
(Ⅱ)当函数f(x)的定义域是[0,1]时,求函数f(x)的值域.
【答案】解:(I)由题意可知ax2+(b﹣8)x﹣a﹣ab=0的两根为﹣3和2,
故可得﹣3+2= ![]() ,﹣3×2=
,﹣3×2= ![]() ,解之可得a=﹣3,b=5
,解之可得a=﹣3,b=5
故可得f(x)=﹣3x2﹣3x+18;
(Ⅱ)由(I)可知,f(x)=﹣3x2﹣3x+18=﹣3 ![]()
图象为开口向下的抛物线,对称轴为x= ![]() ,又x∈[0,1],
,又x∈[0,1],
故函数在x∈[0,1]上单调递减,
故当x=0时,函数取最大值18,当x=1时,函数取最小值12
故所求函数f(x)的值域为[12,18]
【解析】(I)转化为ax2+(b﹣8)x﹣a﹣ab=0的两根为﹣3和2,由韦达定理可得a,b的方程组,解之可得;(Ⅱ)配方可得函数的图象为开口向下的抛物线,对称轴为x= ![]() ,可得函数在x∈[0,1]上单调递减,可得最值.
,可得函数在x∈[0,1]上单调递减,可得最值.
【考点精析】关于本题考查的函数的值域和函数的零点与方程根的关系,需要了解求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的;二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点才能得出正确答案.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知曲线C1的参数方程为 ![]() (φ为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4
(φ为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4 ![]() cosθ.
cosθ.
(1)求C1与C2交点的直角坐标;
(2)已知曲线C3的参数方程为 ![]() (0≤α<π,t为参数,且t≠0),C3与C1相交于点P,C2与C3相交于点Q,且|PQ|=8,求α的值.
(0≤α<π,t为参数,且t≠0),C3与C1相交于点P,C2与C3相交于点Q,且|PQ|=8,求α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F. 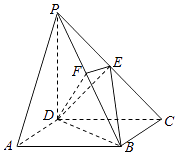
(1)求证:PA∥平面BDE;
(2)求证:PB⊥平面DEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(1﹣x)的定义域为M,函数 ![]() 的定义域为N,则M∩N=( )
的定义域为N,则M∩N=( )
A.{x|x<1且x≠0}
B.{x|x≤1且x≠0}
C.{x|x>1}
D.{x|x≤1}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为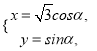 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,求
上,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com