
【题目】![]() ABC的三个角A,B,C所对的边分别是a,b,c,向量
ABC的三个角A,B,C所对的边分别是a,b,c,向量![]() =(2,-1),
=(2,-1),![]() =(sinBsinC,
=(sinBsinC,![]() +2cosBcosC),且
+2cosBcosC),且![]() ⊥
⊥![]() .
.
(1)求角A的大小;
(2)现给出以下三个条件:①B=45;②2sinC-(![]() +1)sinB=0;③a=2.试从中再选择两个条件以确定
+1)sinB=0;③a=2.试从中再选择两个条件以确定![]() ABC,并求出所确定的
ABC,并求出所确定的![]() ABC的面积.
ABC的面积.
【答案】⑴![]() ;⑵选择①,③ S△ABC=
;⑵选择①,③ S△ABC=![]() +1 ;选择②,③ S△ABC=
+1 ;选择②,③ S△ABC=![]() +1; 选择①,②不能确定三角形
+1; 选择①,②不能确定三角形
【解析】
(1)由![]() ⊥
⊥![]() ,可得
,可得![]() ,得cosA=
,得cosA=![]() ,即可得出;
,即可得出;
(2)选择①,③或选择②,③.利用正弦定理与余弦定理、三角形的面积计算公式即可得出.选择①,②不能确定三角形.
(1)∵![]() ⊥
⊥![]() ,∴
,∴![]() =2sinBsinC﹣2cosBcosC﹣
=2sinBsinC﹣2cosBcosC﹣![]() =0,∴cos(B+C)=﹣
=0,∴cos(B+C)=﹣![]() ,
,
∴cosA=![]() ,又0°<A<180°,∴A=30°.
,又0°<A<180°,∴A=30°.
(2)选择①,③.∵A═30°,B=45°,C=105°,a=2,且sin105°=sin(45°+60°)=![]() ,
,
c=![]() =
=![]()
,∴S△ABC=![]() acsinB=
acsinB=![]() +1.
+1.
选择②,③.∵A=30°,a=2,∴2sinC=(![]() +1)sinB2c=(
+1)sinB2c=(![]() +1)b,
+1)b,
由余弦定理:a2=4=b2+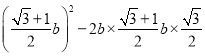 b2=8 b=2
b2=8 b=2![]() .
.
c=![]() ,∴S△ABC=
,∴S△ABC=![]() +1.
+1.
选①,②不能确定三角形.


科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.点(2,0)关于直线y=x+1的对称点为(﹣1,3)
B.过(x1,y1),(x2,y2)两点的直线方程为![]()
C.经过点(1,1)且在x轴和y轴上截距都相等的直线方程为x+y﹣2=0或x﹣y=0
D.直线x﹣y﹣4=0与两坐标轴围成的三角形的面积是8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,离心率等于
轴上,离心率等于![]() ,它的一个顶点恰好在抛物线
,它的一个顶点恰好在抛物线![]() 的准线上.
的准线上.

![]() 求椭圆
求椭圆![]() 的标准方程;
的标准方程;
![]() 点
点![]() ,
,![]() 在椭圆上,
在椭圆上,![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点
两侧的动点![]() 当
当![]() 运动时,满足
运动时,满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥S﹣ABCD中,底面ABCD是边长为4的菱形,∠BAD=60°,SA=SD=2![]() ,点E是棱AD的中点,点F在棱SC上,且
,点E是棱AD的中点,点F在棱SC上,且![]() λ,SA//平面BEF.
λ,SA//平面BEF.
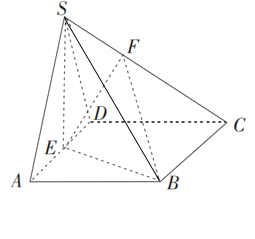
(1)求实数λ的值;
(2)求三棱锥F﹣EBC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别为椭圆
分别为椭圆![]() 右顶点和上顶点,且直线
右顶点和上顶点,且直线![]() 的斜率为
的斜率为![]() ,右焦点
,右焦点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.

![]() 求椭圆
求椭圆![]() 的方程;
的方程;
![]() 若直线
若直线![]()
![]() 与椭圆交于
与椭圆交于![]() 两点,且直线
两点,且直线![]() 的斜率之和为1,求实数
的斜率之和为1,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“我将来要当一名麦田里的守望者,有那么一群孩子在一块麦田里玩,几千万的小孩子,附近没有一个大人,我是说……除了我”《麦田里的守望者》中的主人公霍尔顿将自己的精神生活寄托于那广阔无垠的麦田.假设霍尔顿在一块成凸四边形![]() 的麦田里成为守望者,如图所示,为了分割麦田,他将
的麦田里成为守望者,如图所示,为了分割麦田,他将![]() 连接,设
连接,设![]() 中边
中边![]() 所对的角为
所对的角为![]() ,
,![]() 中边
中边![]() 所对的角为
所对的角为![]() ,经测量已知
,经测量已知![]() ,
,![]() .
.

(1)霍尔顿发现无论![]() 多长,
多长,![]() 为一个定值,请你验证霍尔顿的结论,并求出这个定值;
为一个定值,请你验证霍尔顿的结论,并求出这个定值;
(2)霍尔顿发现麦田的生长于土地面积的平方呈正相关,记![]() 与
与![]() 的面积分别为
的面积分别为![]() 和
和![]() ,为了更好地规划麦田,请你帮助霍尔顿求出
,为了更好地规划麦田,请你帮助霍尔顿求出![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com