
【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”,为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研,人社部从网上年龄在![]() 岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
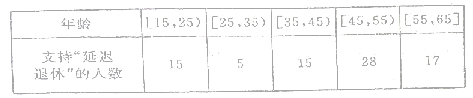
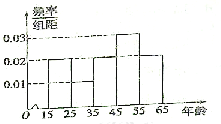
(1)由以上统计数据填![]() 列联表,并判断是否95%的把握认为以
列联表,并判断是否95%的把握认为以![]() 岁为界点的不同人群对“延迟退休年龄政策”的支持有差异;
岁为界点的不同人群对“延迟退休年龄政策”的支持有差异;

(2)若以![]() 岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取
岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取![]() 人参加某项活动,现从这
人参加某项活动,现从这![]() 人中随机抽
人中随机抽![]() 人.
人.
①抽到![]() 人是
人是![]() 岁以下时,求抽到的另一人是
岁以下时,求抽到的另一人是![]() 岁以上的概率;
岁以上的概率;
②记抽到![]() 岁以上的人数为
岁以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
|
|
|
|
|
|
|
|
|
|
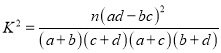
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 的定义域为集合A,函数g(x)=(
的定义域为集合A,函数g(x)=( ![]() )x(﹣1≤x≤0)的值域为集合B.
)x(﹣1≤x≤0)的值域为集合B.
(1)求A∩B;
(2)若集合C=[a,2a﹣1],且C∪B=B,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(ax﹣bx)(a>1>b>0).
(1)求f(x)的定义域;
(2)若f(x)在(1,+∞)上递增且恒取正值,求a,b满足的关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品生产厂家生产一种产品,每生产这种产品x(百台),其总成本为G(x)(万元),其中固定成本为42万元,且每生产1百台的生产成本为15万元(总成本=固定成本+生产成本).销售收入R(x)(万元)满足 ![]() 假定该产品产销平衡(即生产的产品都能卖掉),根据上述规律,完成下列问题:
假定该产品产销平衡(即生产的产品都能卖掉),根据上述规律,完成下列问题:
(1)写出利润函数y=f(x)的解析式(利润=销售收入﹣总成本);
(2)要使工厂有盈利,求产量x的范围;
(3)工厂生产多少台产品时,可使盈利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】问题“求方程5x+12x=13x的解”有如下的思路:方程5x+12x=13x可变为( ![]() )x+(
)x+( ![]() )x=1,考察函数f(x)=(
)x=1,考察函数f(x)=( ![]() )x+(
)x+( ![]() )x可知f(2)=1,且函数f(x)在R上单调递减,所以原方程有唯一解x=2.仿照此解法可得到不等式:lgx﹣4>2lg2﹣x的解集为 .
)x可知f(2)=1,且函数f(x)在R上单调递减,所以原方程有唯一解x=2.仿照此解法可得到不等式:lgx﹣4>2lg2﹣x的解集为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com