
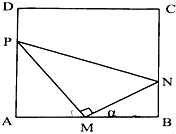
 上海迪士尼乐园有一块长方形地ABCD,若要在此地块上拟建一个Rt△MNP的主题乐园,已知AB=2km,AD=$\sqrt{3}$km,点M是AB的中点,点P在线段AD上,点N在线段BC上,记∠NMB=α.
上海迪士尼乐园有一块长方形地ABCD,若要在此地块上拟建一个Rt△MNP的主题乐园,已知AB=2km,AD=$\sqrt{3}$km,点M是AB的中点,点P在线段AD上,点N在线段BC上,记∠NMB=α.分析 (1)设AP=y,BN=x,由互余的正切互为倒数,求得$\frac{π}{6}$≤α≤$\frac{π}{3}$,再由解直角三角形,可得三角形MNP的面积,再由二倍角公式和正弦函数的性质,即可得到最大值;
(2)运用勾股定理可得NP,求得周长l的表达式,令sinα+cosα=t,求得t的范围,再由同角的平方关系,可得l关于t的函数式,即可得到最大值.
解答 解:(1)设AP=y,BN=x,
由题意可得,tanα•tan∠PMA=$\frac{BN}{BM}$•$\frac{PA}{AM}$=xy=1,
由y=$\frac{1}{x}$可得$\frac{\sqrt{3}}{3}$≤x≤$\sqrt{3}$,
即$\frac{π}{6}$≤α≤$\frac{π}{3}$,
在直角三角形MNP中,MN=$\frac{BM}{cosα}$=$\frac{1}{cosα}$,
MP=$\frac{AM}{sinα}$=$\frac{1}{sinα}$,
则S=$\frac{1}{2}$•$\frac{1}{sinα}$•$\frac{1}{cosα}$=$\frac{1}{sin2α}$,
由$\frac{π}{3}$≤2α≤$\frac{2π}{3}$,sin2α∈[$\frac{\sqrt{3}}{2}$,1].
即有当α=$\frac{π}{6}$或$\frac{π}{3}$时,S取得最大值$\frac{2\sqrt{3}}{3}$;
(2)由(1)可得MN=$\frac{1}{cosα}$,MP=$\frac{1}{sinα}$,
NP=$\sqrt{\frac{1}{co{s}^{2}α}+\frac{1}{si{n}^{2}α}}$=$\frac{1}{sinαcosα}$,
即有l=$\frac{1}{sinα}$+$\frac{1}{cosα}$+$\frac{1}{sinαcosα}$($\frac{π}{6}$≤α≤$\frac{π}{3}$),
=$\frac{sinα+cosα+1}{sinαcosα}$,
令sinα+cosα=t,即t=$\sqrt{2}$sin(α+$\frac{π}{4}$),
由$\frac{π}{6}$≤α≤$\frac{π}{3}$,可得α+$\frac{π}{4}$∈[$\frac{5π}{12}$,$\frac{7π}{12}$],
可得sin(α+$\frac{π}{4}$)∈[$\frac{\sqrt{6}+\sqrt{2}}{4}$,1],
即为t∈[$\frac{\sqrt{3}+1}{2}$,$\sqrt{2}$],
又t2=1+2sinαcosα,可得sinαcosα=$\frac{{t}^{2}-1}{2}$,
则l=$\frac{2(t+1)}{{t}^{2}-1}$=$\frac{2}{t-1}$,
即有当t=$\frac{\sqrt{3}+1}{2}$,即α=$\frac{π}{6}$或$\frac{π}{3}$时,l取得最大值,且为2($\sqrt{3}$+1).
点评 本题考查函数的最值的求法,注意运用三角函数的化简和正弦函数的图象和性质,以及换元后新元的范围,考查运算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{375π}{4}$ | B. | 100π | C. | $\frac{250\sqrt{2}π}{3}$ | D. | $\frac{500π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
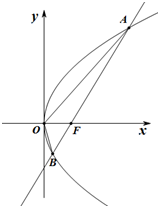 设抛物线C:y2=2px(p>0)的焦点为F,过F且斜率为k的直线l交抛物线C于A(x1,y1),B(x2,y2)两点,且y1y2=-4.
设抛物线C:y2=2px(p>0)的焦点为F,过F且斜率为k的直线l交抛物线C于A(x1,y1),B(x2,y2)两点,且y1y2=-4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | -3 | C. | $\frac{2}{3}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com