
【题目】求证:点 P(x0,y0) 到直线Ax+By+C=0的距离为![]()
【答案】证明:设Q(x,y) 是直线上任意一点,则 Ax+By+C=0 .因为|PQ|2=(x-x0)2+(y-y0)2, ![]() ,由柯西不等式,得
,由柯西不等式,得![]()
![]()
![]()
![]()
所以![]() .
.
当且仅当![]() 时,取等号,|PQ| 取得最小值
时,取等号,|PQ| 取得最小值 ![]() .
.
因此,点 P(x0,y0) 到直线Ax+By+C =0的距离为 ![]() .
.
【解析】本题主要考查了二维形式的柯西不等式,解决问题的关键是利用二维形式的柯西不等式 ![]() ,取“=”的条件是ad=bc.因此,在解题时,对照柯西不等式,必须弄清要求的问题中相当于柯西不等式中的“a , b , c , d”的数或代数式,否则一般出错.
,取“=”的条件是ad=bc.因此,在解题时,对照柯西不等式,必须弄清要求的问题中相当于柯西不等式中的“a , b , c , d”的数或代数式,否则一般出错.
【考点精析】本题主要考查了二维形式的柯西不等式的相关知识点,需要掌握二维形式的柯西不等式:![]() 当且仅当
当且仅当![]() 时,等号成立才能正确解答此题.
时,等号成立才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex , g(x)=mx2+ax+b,其中m,a,b∈R,e=2.71828…为自然对数的底数. (I)函数h(x)=xf (x),当a=l,b=0时,若函数h(x)与g(x)具有相同的单调区间,求m的值;
(II)记F(x)=f(x)﹣g(x).当a=2,m=0时,若函数F(x)在[﹣1,2]上存在两个不同的零点,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位打字员在两台电脑上各自输入A,B两种类型的文件的部分文字才能使这两类文件成为成品.已知A文件需要甲输入0.5小时,乙输入0.2小时;B文件需要甲输入0.3小时,乙输入0.6小时.在一个工作日中,甲至多只能输入6小时,乙至多只能输入8小时,A文件每份的利润为60元,B文件每份的利润为80元,则甲、乙两位打字员在一个工作日内获得的最大利润是元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(sinx﹣cosx)2+ ![]() sin(2x+
sin(2x+ ![]() )(x∈R).
)(x∈R).
(1)求函数f(x)的递减区间;
(2)若f(α)= ![]() ,α∈(
,α∈( ![]() ,
, ![]() ),求cos(2α+
),求cos(2α+ ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市2010年至2016年新开楼盘的平均销售价格y(单位:千元/平米)的统计数据如表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格y | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
(1)求y关于x的线性回归方程;
(2)利用(Ⅰ)中的回归方程,分析2010年至2016年该市新开楼盘平均销售价格的变化情况,并预测该市2018年新开楼盘的平均销售价格.
附:参考数据及公式: ![]() ,
, 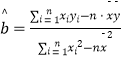 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=1,BC=2,∠CBA= ![]() ,ABEF为直角梯形,BE∥AF,∠BAF=
,ABEF为直角梯形,BE∥AF,∠BAF= ![]() ,BE=2,AF=3,平面ABCD⊥平面ABEF.
,BE=2,AF=3,平面ABCD⊥平面ABEF.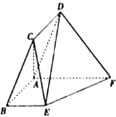
(1)求证:AC⊥平面ABEF;
(2)求平面ABCD与平面DEF所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是内角A,B,C的对边,且(a+c)2=b2+3ac
(Ⅰ)求角B的大小;
(Ⅱ)若b=2,且sinB+sin(C﹣A)=2sin2A,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com