
【题目】无穷等差数列![]() 的各项均为整数,首项为
的各项均为整数,首项为![]() 、公差为
、公差为![]() ,
,![]() 是其前
是其前![]() 项和,
项和,![]() 是其中的三项,给出下列命题:
是其中的三项,给出下列命题:
①对任意满足条件的![]() ,存在
,存在![]() ,使得
,使得![]() 一定是数列
一定是数列![]() 中的一项;
中的一项;
②存在满足条件的数列![]() ,使得对任意的
,使得对任意的![]() ,
,![]() 成立;
成立;
③对任意满足条件的![]() ,存在
,存在![]() ,使得
,使得![]() 一定是数列
一定是数列![]() 中的一项。
中的一项。
其中正确命题的序号为( )
A.①②B.②③C.①③D.①②③
【答案】A
【解析】
利用等差数列的公式,分别讨论前![]() 项和
项和![]() 的具体项数,然后进行推理即可,首先根据条件得出
的具体项数,然后进行推理即可,首先根据条件得出![]() ;①
;①![]() 能被
能被![]() 整除,且为
整除,且为![]() ,假设
,假设![]() 和
和![]() 之间有
之间有![]() 项,那么
项,那么![]() 和
和![]() 之间有
之间有![]() 项,得出结论;
项,得出结论;
②利用等差数列的前![]() 项和公式化简
项和公式化简![]() ,得出结论;
,得出结论;
③![]() 不能被
不能被![]() 整除,如果
整除,如果![]() ,那么
,那么![]() 一定不是数列
一定不是数列![]() 中的一项,得出结论.
中的一项,得出结论.
要使等差数列的公差最大,则![]() 为相邻的前
为相邻的前![]() 项和,此时对应两项为
项和,此时对应两项为![]() ,
,![]() ,所以
,所以![]() .
.
①![]() 能被
能被![]() 整除,且
整除,且![]() ,假设
,假设![]() 和
和![]() 之间有
之间有![]() 项,
项,
那么![]() 和
和![]() 之间有
之间有![]() 项,所以
项,所以![]() 一定是数列
一定是数列![]() 中的一项,所以①正确;
中的一项,所以①正确;
②如果有![]() ,那么由等差数列求和公式有:
,那么由等差数列求和公式有:![]()
 ,化简得到,
,化简得到,![]() ,所以只要满足条件
,所以只要满足条件![]() 的数列
的数列![]() ,
,
就能使得对任意的![]() ,
,![]() 成立,所以②正确;
成立,所以②正确;
③![]() 不能被
不能被![]() 整除,如果
整除,如果![]() ,那么
,那么![]() 一定不是数列
一定不是数列![]() 中的一项,所以③错误.
中的一项,所以③错误.
综上可得:只有①②正确.
故选:A.


科目:高中数学 来源: 题型:
【题目】随着社会的进步与发展,中国的网民数量急剧增加.下表是中国从![]() 年网民人数及互联网普及率、手机网民人数(单位:亿)及手机网民普及率的相关数据.
年网民人数及互联网普及率、手机网民人数(单位:亿)及手机网民普及率的相关数据.
年份 | 网民人数 | 互联网普及率 | 手机网民人数 | 手机网民普及率 |
2009 |
|
|
|
|
2010 |
|
|
|
|
2011 |
|
|
|
|
2012 |
|
|
|
|
2013 |
|
|
|
|
2014 |
|
|
|
|
2015 |
|
|
|
|
2016 |
|
|
|
|
2017 |
|
|
|
|
2018 |
|
|
|
|
(互联网普及率![]() (网民人数/人口总数)×100%;手机网民普及率
(网民人数/人口总数)×100%;手机网民普及率![]() (手机网民人数/人口总数)×100%)
(手机网民人数/人口总数)×100%)
(Ⅰ)从![]() 这十年中随机选取一年,求该年手机网民人数占网民总人数比值超过80%的概率;
这十年中随机选取一年,求该年手机网民人数占网民总人数比值超过80%的概率;
(Ⅱ)分别从网民人数超过6亿的年份中任选两年,记![]() 为手机网民普及率超过50%的年数,求
为手机网民普及率超过50%的年数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)若记![]() 年中国网民人数的方差为
年中国网民人数的方差为,手机网民人数的方差为
![]() ,试判断
,试判断![]() 与
与![]() 的大小关系.(只需写出结论)
的大小关系.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心坐标为
的圆心坐标为![]() ,且该圆经过点
,且该圆经过点![]() .
.
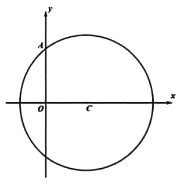
(1)求圆![]() 的标准方程;
的标准方程;
(2)若点![]() 也在圆
也在圆![]() 上,且弦
上,且弦![]() 长为8,求直线
长为8,求直线![]() 的方程;
的方程;
(3)直线![]() 交圆
交圆![]() 于
于![]() ,
,![]() 两点,若直线
两点,若直线![]() ,
,![]() 的斜率之积为2,求证:直线
的斜率之积为2,求证:直线![]() 过一个定点,并求出该定点坐标.
过一个定点,并求出该定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体ABCD-A1B1C1D1中(如图),AD=AA1=1,AB=2,点E是棱AB的中点.
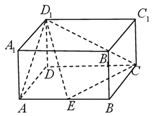
(1)求异面直线AD1与EC所成角的大小;
(2)《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑,试问四面体D1CDE是否为鳖臑?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设O为坐标原点,动点M在椭圆C![]() 上,过M作x轴的垂线,垂足为N,点P满足
上,过M作x轴的垂线,垂足为N,点P满足![]() .
.
(1)求点P的轨迹方程;
(2)设点![]() 在直线
在直线![]() 上,且
上,且![]() .证明:过点P且垂直于OQ的直线
.证明:过点P且垂直于OQ的直线![]() 过C的左焦点F.
过C的左焦点F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于曲线![]() ,有如下结论:
,有如下结论:
①曲线C关于原点对称;
②曲线C关于直线x±y=0对称;
③曲线C是封闭图形,且封闭图形的面积大于2π;
④曲线C不是封闭图形,且它与圆x2+y2=2无公共点;
⑤曲线C与曲线![]() 有4个交点,这4点构成正方形.其中所有正确结论的序号为__.
有4个交点,这4点构成正方形.其中所有正确结论的序号为__.
查看答案和解析>>
科目:高中数学 来源: 题型:
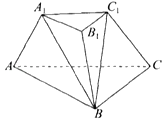
【题目】如图,在三棱台ABC﹣A1B1C1中,底面ABC是边长为2的等边三角形,上、下底面的面积之比为1:4,侧面A1ABB1⊥底面ABC,并且A1A=A1B1,∠AA1B=90°.
(1)平面A1C1B∩平面ABC=l,证明:A1C1∥l;
(2)求平面A1C1B与平面ABC所成二面角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com