
【题目】符号![]() 表示不大于
表示不大于![]() 的最大整数(
的最大整数(![]() ),例如:
),例如:![]()
(1)已知![]() ,分别求两方程的解集
,分别求两方程的解集![]() ;
;
(2)设方程![]() 的解集为
的解集为![]() ,集合
,集合![]() ,若
,若![]() ,求
,求![]() 的取值范围.
的取值范围.
(3)在(2)的条件下,集合![]() ,是否存在实数
,是否存在实数![]() ,
,![]() ,若存在,请求出实数
,若存在,请求出实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】2018年6月14日,第二十一届世界杯尼球赛在俄罗斯拉开了帷幕,某大学在二年级作了问卷调查,从该校二年级学生中抽取了![]() 人进行调查,其中女生中对足球运动有兴趣的占
人进行调查,其中女生中对足球运动有兴趣的占![]() ,而男生有
,而男生有![]() 人表示对足球运动没有兴趣.
人表示对足球运动没有兴趣.
(1)完成![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“对足球是否有兴趣与性别有关”?
的把握认为“对足球是否有兴趣与性别有关”?
有兴趣 | 没有兴趣 | 合计 | |
男 |
| ||
女 | |||
合计 |
(2)若将频率视为概率,现再从该校二年级全体学生中,采用随机抽样的方法每饮抽取![]() 名学生,抽取
名学生,抽取![]() 次,记被抽取的
次,记被抽取的![]() 名学生中对足球有兴趣的人数为
名学生中对足球有兴趣的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
|
|
|
|
|
|
|
|
|
|
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一款手机,每部购买费用是5000元,每年网络费和电话费共需1000元;每部手机第一年不需维修,第二年维修费用为100元,以后每一年的维修费用均比上一年增加100元.设该款手机每部使用![]() 年共需维修费用
年共需维修费用![]() 元,总费用
元,总费用![]() 元.(总费用
元.(总费用![]() 购买费用
购买费用![]() 网络费和电话费
网络费和电话费![]() 维修费用)
维修费用)
(1)求函数![]() 、
、![]() 的表达式:
的表达式:
(2)这款手机每部使用多少年时,它的年平均费用最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1: ![]() +y2=1,椭圆C2以C1的长轴为短轴,且与C1有相同的离心率.
+y2=1,椭圆C2以C1的长轴为短轴,且与C1有相同的离心率.
(1)求椭圆C2的方程;
(2)设O为坐标原点,点A,B分别在椭圆C1和C2上, ![]() =2
=2 ![]() ,求直线AB的方程.
,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心为![]() 的圆过点
的圆过点![]() ,且与直线
,且与直线![]() 相切于点
相切于点![]() 。
。
(1)求圆![]() 的方程;
的方程;
(2)已知点![]() ,且对于圆
,且对于圆![]() 上任一点
上任一点![]() ,线段
,线段![]() 上存在异于点
上存在异于点![]() 的一点
的一点![]() ,使得
,使得![]() (
(![]() 为常数),试判断使
为常数),试判断使![]() 的面积等于4的点
的面积等于4的点![]() 有几个,并说明理由。
有几个,并说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】足球,有“世界第一运动的美誉,是全球体育界最具影响力的单项体育运动之一.足球传球是足球运动技术之一,是比赛中组织进攻、组织战术配合和进行射门的主要手段.足球截球也是足球运动技术的一种,是将对方控制或传出的球占为己有,或破坏对方对球的控制的技术,是比赛中由守转攻的主要手段.这两种运动技术都需要球运动员的正确判断和选择.现有甲、乙两队进行足球友谊赛,A、B两名运动员是甲队队员,C是乙队队员,B在A的正西方向,A和B相距20m,C在A的正北方向,A和C相距14![]() m.现A沿北偏西60°方向水平传球,球速为10
m.现A沿北偏西60°方向水平传球,球速为10![]() m/s,同时B沿北偏西30°方向以10m/s的速度前往接球,C同时也以10m/s的速度前去截球.假设球与B、C都在同一平面运动,且均保持匀速直线运动.
m/s,同时B沿北偏西30°方向以10m/s的速度前往接球,C同时也以10m/s的速度前去截球.假设球与B、C都在同一平面运动,且均保持匀速直线运动.
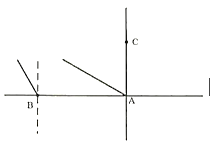
(1)若C沿南偏西60°方向前去截球,试判断B能否接到球?请说明理由.
(2)若C改变(1)的方向前去截球,试判断C能否球成功?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭10次,命中的环数如下:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)计算甲、乙两人射箭命中环数的平均数和标准差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知函数f(x)=![]()
(1)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论.
(2)求该函数在区间[1,4]上的最大值与最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com