
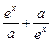 是R上的偶函数,(1)求a的值;(2)证明: f(x)在(0,+∞)上是增函数.
是R上的偶函数,(1)求a的值;(2)证明: f(x)在(0,+∞)上是增函数. 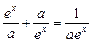 +aex
+aex 整理,得(a-
整理,得(a-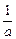 )(ex-
)(ex-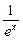 )=0.
)=0. 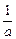 =0,即a2=1,又a>0,∴a=1.
=0,即a2=1,又a>0,∴a=1. 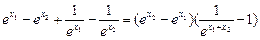
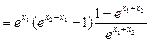
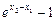 >0,1-e
>0,1-e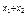 <0,
<0,

科目:高中数学 来源:不详 题型:解答题
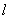 上,
上,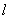 与水平地面的夹角为a ,tana=1/2试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)
与水平地面的夹角为a ,tana=1/2试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)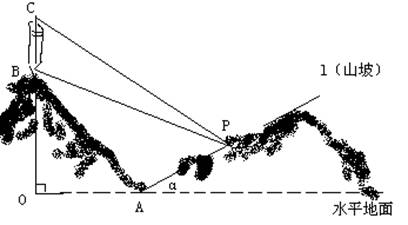
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
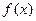 =
=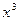 +a
+a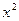 +b的图象在点P (1,0)处的切线与直线3x+y=0平行.则a、b的值分别为( ).
+b的图象在点P (1,0)处的切线与直线3x+y=0平行.则a、b的值分别为( ).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 =x.
=x. 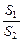 的解析式并求f(x)的定义域.
的解析式并求f(x)的定义域. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
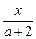 =|a-1|+2的根的取值范围.
=|a-1|+2的根的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com