
【题目】设m,n为平面α外两条直线,其在平面α内的射影分别是两条直线m1和n1,给出下列4个命题:①m1∥n1m∥n;②m∥nm1与n1平行或重合;③m1⊥n1m⊥n;④m⊥nm1⊥n1.其中所有假命题的序号是_____.
科目:高中数学 来源: 题型:
【题目】有![]() 名学生排成一排,求分别满足下列条件的排法种数,要求列式并给出计算结果.
名学生排成一排,求分别满足下列条件的排法种数,要求列式并给出计算结果.
(1)甲不在两端;
(2)甲、乙相邻;
(3)甲、乙、丙三人两两不得相邻;
(4)甲不在排头,乙不在排尾。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是函数
是函数![]() 的图象上的一点,等比数列
的图象上的一点,等比数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]()
![]() 的首项为
的首项为![]() ,且前
,且前![]() 项和
项和![]() 满足:
满足:![]() .
.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)若数列![]() 的通项
的通项 ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若数列 的前项和为
的前项和为![]() ,是否存在最大的整数
,是否存在最大的整数![]() ,使得对任意的正整数n,均有
,使得对任意的正整数n,均有![]() 总成立?若成立,求出t;若不存在,请说明理由.
总成立?若成立,求出t;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某种细菌的适宜生长温度为![]() ,为了研究该种细菌的繁殖数量
,为了研究该种细菌的繁殖数量![]() (单位:个)随温度
(单位:个)随温度![]() (单位:
(单位:![]() )变化的规律,收集数据如下:
)变化的规律,收集数据如下:
温度 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
繁殖数量 | 20 | 25 | 33 | 27 | 51 | 112 | 194 |
对数据进行初步处理后,得到了一些统计量的值,如下表所示:
|
|
|
|
|
|
|
18 | 66 | 3.8 | 112 | 4.3 | 1428 | 20.5 |
其中![]() ,
,![]() .
.
(1)请绘出![]() 关于
关于![]() 的散点图,并根据散点图判断
的散点图,并根据散点图判断![]() 与
与![]() 哪一个更适合作为该种细菌的繁殖数量
哪一个更适合作为该种细菌的繁殖数量![]() 关于
关于![]() 的回归方程类型(结果精确到0.1);
的回归方程类型(结果精确到0.1);
(2)当温度为![]() 时,该种细菌的繁殖数量的预报值为多少?
时,该种细菌的繁殖数量的预报值为多少?
参考公式:对于一组数据![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: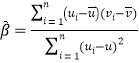 ,
,![]() .参考数据:
.参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网站用“100分制”调查一社区人们的幸福度.现从调查人群中随机抽取10名,以下茎叶图记录了他们的幸福度分数(以十位数字为茎,个位数字为叶);若幸福度不低于95分,则称该人的幸福度为“极幸福”.

(1)从这10人中随机选取3人,记![]() 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)以这10人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记![]() 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求![]() 的数学期望和方差.
的数学期望和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一半径为![]() 的水轮,水轮圆心
的水轮,水轮圆心![]() 距离水面2
距离水面2![]() ,已知水轮每分钟转动(按逆时针方向)3圈,当水轮上点
,已知水轮每分钟转动(按逆时针方向)3圈,当水轮上点![]() 从水中浮现时开始计时,即从图中点
从水中浮现时开始计时,即从图中点![]() 开始计算时间.
开始计算时间.

(1)当![]() 秒时点
秒时点![]() 离水面的高度_________;
离水面的高度_________;
(2)将点![]() 距离水面的高度
距离水面的高度![]() (单位:
(单位: ![]() )表示为时间
)表示为时间![]() (单位:
(单位: ![]() )的函数,则此函数表达式为_______________ .
)的函数,则此函数表达式为_______________ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com