
如图,已知正方形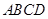 的边长为1,
的边长为1,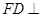 平面
平面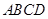 ,
, 平面
平面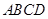 ,
, 为
为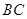 边上的动点。
边上的动点。
(1)证明: 平面
平面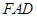 ;
;
(2)试探究点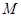 的位置,使平面
的位置,使平面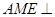 平面
平面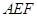 。
。

解:(1)∵ FD⊥平面ABCD,EB⊥平面ABCD
∴FD∥EB
又AD∥BC且AD∩FD=D,BC∩BE=B
∴平面FAD∥平面EBC,ME  平面EBC
平面EBC
∴ME∥平面FAD ……………………4分
(2)以D为坐标原点,分别以DA、DC、DF所在直线为x、y、z轴,建立空间直角坐标D-xyz,
依题意,得D(0,0,0),A(1,0,0),F(0,0,1),C(0,1,0),B(1,1,0),E(1,1,1),
设M(λ,1,0),平面AEF的法向量为 =(x1,y1,z1),平面AME的法向量为
=(x1,y1,z1),平面AME的法向量为 =(x2,y2,z2)
=(x2,y2,z2)
∵ =(0,1,1),
=(0,1,1), =(-1,0,1), ∴
=(-1,0,1), ∴ ∴
∴
取z1=1,得x1=1,y1=-1 ∴ =(1,-1,0)
=(1,-1,0)
又 =(λ-1,1,0) ,
=(λ-1,1,0) , =(0,1,1),
=(0,1,1),
∴ ∴
∴
取x2=1得y2=1-λ,z2=λ-1 ∴  =(1,1-λ,λ-1)
=(1,1-λ,λ-1)
若平面AME⊥平面AEF,则 ⊥
⊥ ∴
∴
 =0,
=0,
∴1-(1-λ)+(λ-1)=0,解得λ= ,
,
此时M为BC的中点.
所以当M在BC的中点时, AME⊥平面AEF. ……………12分
【解析】略


科目:高中数学 来源: 题型:
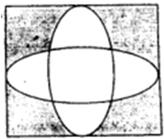 如图,已知正方形的边长为10,向正方形内随机地撒200颗黄豆,数得落在阴影外的黄豆数为114颗,以此实验数据为依据,可以估计出阴影部分的面积约为( )
如图,已知正方形的边长为10,向正方形内随机地撒200颗黄豆,数得落在阴影外的黄豆数为114颗,以此实验数据为依据,可以估计出阴影部分的面积约为( )| A、53 | B、43 | C、47 | D、57 |
查看答案和解析>>
科目:高中数学 来源: 题型:
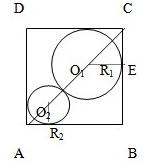 如图,已知正方形的边长为1,在正方形ABCD中有两个相切的内切圆.
如图,已知正方形的边长为1,在正方形ABCD中有两个相切的内切圆.查看答案和解析>>
科目:高中数学 来源: 题型:
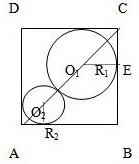 第8题的题干为:如图,已知正方形的边长为1,在正方形ABCD中有两个相切的内切圆.
第8题的题干为:如图,已知正方形的边长为1,在正方形ABCD中有两个相切的内切圆.查看答案和解析>>
科目:高中数学 来源:2014届福建省高二上学期期末考试理科数学试卷(解析版) 题型:选择题
如图,已知正方形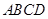 的边长为
的边长为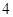 ,
,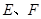 分别是
分别是 的中点,
的中点,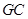 ⊥平面
⊥平面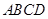 ,且
,且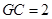 ,则点
,则点 到平面
到平面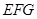 的距离为
的距离为

A. B.
B. C.
C.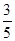 D.1
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com