
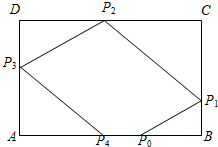
 如图,矩形ABCD中,AB=3,AD=2,一质点从AB边上的点P0出发,沿与AB的夹角为θ的方向射到边BC上点P1后,依次反射(入射角与反射角相等)到边CD,DA和AB上的P2,P3,P4处.
如图,矩形ABCD中,AB=3,AD=2,一质点从AB边上的点P0出发,沿与AB的夹角为θ的方向射到边BC上点P1后,依次反射(入射角与反射角相等)到边CD,DA和AB上的P2,P3,P4处.分析 (1)设P0B=m(0<m<3),给出P1B、P1C关于m和tanθ的式子,利用解直角三角形分别算出P2C、P2D、P3D、P3A,从而可得AP4=$\frac{{P}_{3}A}{tanθ}$=$\frac{4}{tanθ}$,根据点P4与P0重合得AP4+P0B=3,化成关于tanθ的式子,可得tanθ的值;
(2)(i)当AP0=2即m=1,结合(I)得AP4=$\frac{4}{t}$.由P4落在A,P0两点之间解得0<AP4<2,从而tanθ=t∈($\frac{2}{3}$,1);
(ii)由五边形面积S=SABCD-${S}_{△B{P}_{0}{P}_{1}}$-${S}_{△C{P}_{1}{P}_{2}}$-${S}_{△D{P}_{2}{P}_{3}}$-${S}_{△A{P}_{3}{P}_{4}}$,将S化成关于t的函数S=32-(17t+$\frac{12}{t}$),再利用基本不等式求最值可得当t=$\sqrt{\frac{12}{17}}$时,S的最大值为32-4$\sqrt{51}$.
解答 解:(1)设P0B=m(0<m<3),可得:
P1B=mtanθ,P1C=2-mtanθ,
P2C=$\frac{{P}_{1}C}{tanθ}$=$\frac{2}{tanθ}$,P2D=3+m-$\frac{2}{tanθ}$,
∴P3D=P2D•tanθ=(3+m)tanθ-2,P3A=4-(3+m)tanθ,
可得AP4=$\frac{{P}_{3}A}{tanθ}$=$\frac{4}{tanθ}$-3-m,
∵点P4与P0重合,∴AP4+P0B=3,
即$\frac{4}{tanθ}$-3-m+m=3,可得$\frac{4}{tanθ}$=6,解之得tanθ=$\frac{2}{3}$;
(2)(i)当AP0=2即m=1,由(I)可得AP4=$\frac{4}{tanθ}$-4,
∵P4落在A,P0两点之间,可得0<AP4<2,即tanθ=t∈($\frac{2}{3}$,1);
(ii)五边形面积S=SABCD-${S}_{△B{P}_{0}{P}_{1}}$-${S}_{△C{P}_{1}{P}_{2}}$-${S}_{△D{P}_{2}{P}_{3}}$-${S}_{△A{P}_{3}{P}_{4}}$
=6-$\frac{1}{2}$t-$\frac{1}{2}$(2-t)($\frac{2}{t}$-1)-$\frac{1}{2}$(4-$\frac{2}{t}$)(4t-2)-$\frac{1}{2}$(4-4t)($\frac{4}{t}$-4)
=32-17t-$\frac{12}{t}$=32-(17t+$\frac{12}{t}$)≤32-2$\sqrt{17t•\frac{12}{t}}$=32-4$\sqrt{51}$,
由此可得:当且仅当t=$\sqrt{\frac{12}{17}}$时,S的最大值为32-4$\sqrt{51}$.
点评 本题给出实际应用问题,求函数五边形面积的最大值.着重考查了解直角三角形、三角形的面积公式和利用基本不等式求函数的最值等知识,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
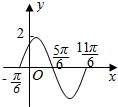 如图是$y=Asin(ωx+φ)(A>0,ω>0,0<φ<\frac{π}{2})$的图象,则其解析式为$y=2sin(x+\frac{π}{6})$.
如图是$y=Asin(ωx+φ)(A>0,ω>0,0<φ<\frac{π}{2})$的图象,则其解析式为$y=2sin(x+\frac{π}{6})$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com