
【题目】已知函数![]() .
.
(1)若曲线![]() 在点
在点![]() 处与直线
处与直线![]() 相切,求
相切,求![]() 的值;
的值;
(2)若函数![]() 有两个零点
有两个零点![]() ,试判断
,试判断![]() 的符号,并证明.
的符号,并证明.
【答案】(1) ![]() ;(2) 当
;(2) 当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
【解析】
试题分析:(1)求函数![]() 的导数
的导数![]() ,由
,由![]() 可求
可求![]() 的值;(2)由(1)可知
的值;(2)由(1)可知![]() ,且定义域为
,且定义域为![]() ,先讨论当
,先讨论当![]() 时
时![]() 的零点是否符合题意,当
的零点是否符合题意,当![]() 时,由
时,由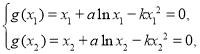 ,两式作差并整理得
,两式作差并整理得![]() ,则
,则![]() ,设
,设![]() ,
,![]() ,
,![]() ,,所以有
,,所以有![]() ,构造函数
,构造函数![]() ,讨论函数
,讨论函数![]() 的单调性与符号,可知
的单调性与符号,可知![]() 的符号.
的符号.
试题解析: (1)![]() ,又∵
,又∵![]() .………………2分
.………………2分
所以![]() .………………3分
.………………3分
(2)函数![]() 的定义域是
的定义域是![]() .………………4分
.………………4分
若![]() ,则
,则![]() .
.
令![]() ,则
,则![]() .
.
又据题设分析知![]() ,
,
∴![]() ,
,![]() .
.
又![]() 有两个零点,且都大于0,
有两个零点,且都大于0,
∴![]() ,不成立.………………5分
,不成立.………………5分
据题设知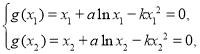
不妨设![]() ,
,![]() ,
,![]() .………………6分
.………………6分
所以![]() .
.
所以![]() .………………7分
.………………7分
又![]() ,
,
所以![]()
![]() .………………9分
.………………9分
引入![]() ,则
,则![]() .
.
所以![]() 在
在![]() 上单调递减.………………10分
上单调递减.………………10分
而![]() ,所以当
,所以当![]() 时,
时,![]() .
.
易知![]() ,
,![]() ,
,
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .………………12分
.………………12分


科目:高中数学 来源: 题型:
【题目】随机抽取了40辆汽车在经过路段上某点是的车速(![]() ),现将其分成六段:
),现将其分成六段:![]() ,
,
![]() 后得到如图所示的频率分布直方图.
后得到如图所示的频率分布直方图.
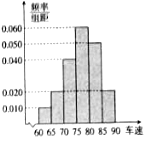
(I)现有某汽车途经该点,则其速度低于80![]() 的概率约是多少?
的概率约是多少?
(II)根据频率分布直方图,抽取的40辆汽车经过该点的平均速度是多少?
(III)在抽取的40辆汽车且速度在![]() (
(![]() )内的汽车中任取2辆,求这2辆车车速都在
)内的汽车中任取2辆,求这2辆车车速都在![]() (
(![]() )内的概率.
)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长时间用手机上网严重影响着学生的身体健康,某校为了解![]() 两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中茎叶表示十位数字,叶表示个位数字).
两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中茎叶表示十位数字,叶表示个位数字).
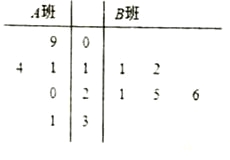
(1)分别求出图中所给两组样本数据的平均值,并据此估计,哪个班的学生平均上网时间较长;
(2)从![]() 班的样本数据中随机抽取一个不超过19的数据记为
班的样本数据中随机抽取一个不超过19的数据记为![]() ,从
,从![]() 班的样本数据中随机抽取一个不超过21的数据记为
班的样本数据中随机抽取一个不超过21的数据记为![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《续古摘奇算法》(杨辉)一书中有关于三阶幻方的问题:将1,2,3,4,5,6,7,8,9分别填入![]() 的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
8 | 3 | 4 |
1 | 5 | 9 |
6 | 7 | 2 |
A. 9 B. 8 C. 6 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知以
中,已知以![]() 为圆心的圆
为圆心的圆![]() 及其上一点
及其上一点![]() .
.

(1)是否存在直线![]() 与圆
与圆![]() 有两个交点
有两个交点![]() ,并且
,并且![]() ,若有,求此直线方程,若没有,请说明理由;
,若有,求此直线方程,若没有,请说明理由;
(2)设点![]() 满足:存在圆
满足:存在圆![]() 上的两点
上的两点![]() 和
和![]() 使得
使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,设倾斜角为
中,设倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数)与曲线
为参数)与曲线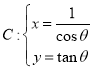 (
(![]() 为参数)相交于不同的两点
为参数)相交于不同的两点![]() .
.
(1)若![]() ,求线段
,求线段![]() 的中点的直角坐标;
的中点的直角坐标;
(2)若直线![]() 的斜率为2,且过已知点
的斜率为2,且过已知点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com