
【题目】已知椭圆C:![]() 1(a>b>0)的离心率为
1(a>b>0)的离心率为![]() ,点M(a,0),N(0,b),O(0,0),且△OMN的面积为1.
,点M(a,0),N(0,b),O(0,0),且△OMN的面积为1.
(1)求椭圆C的标准方程;
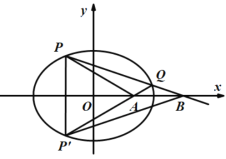
(2)设A,B是x轴上不同的两点,点A(异于坐标原点)在椭圆C内,点B在椭圆C外.若过点B作斜率不为0的直线与C相交于P,Q两点,且满足∠PAB+∠QAB=180°.证明:点A,B的横坐标之积为定值.
【答案】(1)![]() y2=1;(2)见解析
y2=1;(2)见解析
【解析】
(1)由题意离心率的值及三角形OMN的面积和a,b,c之间的关系求出a,b的值,进而求出椭圆的方程;
(2)作点P关于x轴的对称点![]() ,由椭圆的对称性可知∠PAB=∠
,由椭圆的对称性可知∠PAB=∠![]() AB,∠QBA=∠
AB,∠QBA=∠![]() BA,所以
BA,所以![]() ,A,Q三点共线,设
,A,Q三点共线,设![]() Q,A,B的坐标,设直线
Q,A,B的坐标,设直线![]() Q的方程与椭圆联立求出两根之和及两根之积,因为∠QBA=∠
Q的方程与椭圆联立求出两根之和及两根之积,因为∠QBA=∠![]() BA,所以
BA,所以![]() ,求出两条直线的斜率,求出A,B的乘积为定值.
,求出两条直线的斜率,求出A,B的乘积为定值.
解:(1)由题意可得: ,解得:a2=4,b2=1,
,解得:a2=4,b2=1,
所以椭圆C的标准方程:![]() y2=1;
y2=1;
(2)证明:作点P关于x轴的对称点![]() ,由椭圆的对称性可知,
,由椭圆的对称性可知,
点![]() 在椭圆上,且∠PAB=∠
在椭圆上,且∠PAB=∠![]() AB,∠QBA=∠
AB,∠QBA=∠![]() BA,
BA,
因为∠PAB+∠QAB=180°.所以∠![]() AB+∠QAB=180°,
AB+∠QAB=180°,
所以![]() ,A,Q三点共线,
,A,Q三点共线,
由题意可知直线![]() Q不与x轴平行或重合,设直线
Q不与x轴平行或重合,设直线![]() Q的方程为:x=ty+m,(mt≠0),
Q的方程为:x=ty+m,(mt≠0),
设![]() ,
,
联立直线与椭圆的方程:![]() ,消x可得
,消x可得![]() ,
,
则有y1+y2![]() ,y1y2
,y1y2![]() ,
,
因为∠QBA=∠![]() BA,所以
BA,所以![]() ,即
,即![]() ,
,
所以![]() ,
,
即![]()
即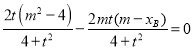 ,
,
解得![]() ,
,
因为![]() ,所以
,所以![]() ,
,
故点A,B横坐标之积为定值4.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
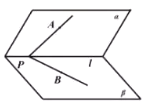
【题目】如图,二面角![]() 中,
中,![]() ,射线
,射线![]() ,
,![]() 分别在平面
分别在平面![]() ,
,![]() 内,点A在平面
内,点A在平面![]() 内的射影恰好是点B,设二面角
内的射影恰好是点B,设二面角![]() 、
、![]() 与平面
与平面![]() 所成角、
所成角、![]() 与平面
与平面![]() 所成角的大小分别为
所成角的大小分别为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高二某班共有45人,学号依次为1、2、3、…、45,现按学号用系统抽样的办法抽取一个容量为5的样本,已知学号为6、24、33的同学在样本中,那么样本中还有两个同学的学号应为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为2,且过点
的焦距为2,且过点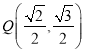 .
.
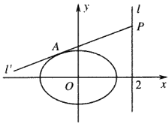
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 为坐标原点,
为坐标原点,![]() 为直线
为直线![]() 上的一动点,过点
上的一动点,过点![]() 作直线
作直线![]() 与椭圆相切于点
与椭圆相切于点![]() ,若
,若![]() 的面积
的面积![]() 为
为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大以来,某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求,带领广大农村地区人民群众脱贫奔小康.经过不懈的奋力拼搏,新农村建设取得巨大进步,农民年收入也逐年增加,为了制定提升农民收入、实现2020年脱贫的工作计划,该地扶贫办统计了2019年50位农民的年收入并制成如下频率分布直方图:
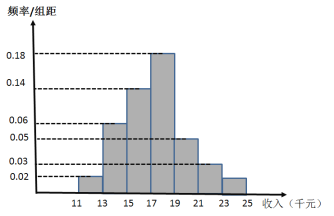
(1)根据频率分布直方图,估计50位农民的平均年收入![]() (单位:千元);(同一组数据用该组数据区间的中点值表示);
(单位:千元);(同一组数据用该组数据区间的中点值表示);
(2)由频率分布直方图,可以认为该贫困地区农民年收入X服从正态分布![]() ,其中
,其中![]() 近似为年平均收入
近似为年平均收入![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经计算得
,经计算得![]() =6.92,利用该正态分布,求:
=6.92,利用该正态分布,求:
①在扶贫攻坚工作中,若使该地区约有占总农民人数的![]() 的农民的年收入高于扶贫办制定的最低年收入标准,则最低年收入标准大约为多少千元?
的农民的年收入高于扶贫办制定的最低年收入标准,则最低年收入标准大约为多少千元?
②为了调研“精准扶贫,不落一人”的政策要求落实情况,扶贫办随机走访了1000位农民.若每位农民的年收入互相独立,问:这1000位农民中的年收入不少于12.14千元的人数最有可能是多少?
附参考数据:![]() ,若随机变量X服从正态分布
,若随机变量X服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,已知
,已知![]() 是以
是以![]() 为底边,且边
为底边,且边![]() 平行于
平行于![]() 轴的等腰三角形.
轴的等腰三角形.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知直线![]() 交
交![]() 轴于点
轴于点![]() ,且与曲线
,且与曲线![]() 相切于点
相切于点![]() ,点
,点![]() 在曲线
在曲线![]() 上,且直线
上,且直线![]() 轴,点
轴,点![]() 关于点
关于点![]() 的对称点为点
的对称点为点![]() ,试判断点
,试判断点![]() 、
、![]() 、
、![]() 三点是否共线,并说明理由.
三点是否共线,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年底,武汉发生“新型冠状病毒”肺炎疫情,国家卫健委紧急部署,从多省调派医务工作者前去支援,正值农历春节举家团圆之际,他们成为“最美逆行者”.武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者疑似的新冠肺炎患者无法明确排除新冠肺炎的发热患者和确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户不漏一人.若在排查期间,某小区有5人被确认为“确诊患者的密切接触者”,现医护人员要对这5人随机进行逐一“核糖核酸”检测,只要出现一例阳性,则将该小区确定为“感染高危小区”.假设每人被确诊的概率均为![]() 且相互独立,若当
且相互独立,若当![]() 时,至少检测了4人该小区被确定为“感染高危小区”的概率取得最大值,则
时,至少检测了4人该小区被确定为“感染高危小区”的概率取得最大值,则![]() ____.
____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com