练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    　D

    [解析]　⊙C1：(x＋a)2＋y2＝4的圆心C1(－a,0)，半径r1＝2，⊙C2：x2＋(y－b)2＝1的圆心C2(0，b)，半径r2＝1，

    ∵⊙C1与⊙C2外切，∴|C1C2|＝r1＋r2，

    ∴a2＋b2＝9，

    ∵(a＋b)2＝a2＋b2＋2ab≤2(a2＋b2)＝18，

    ∴a＋b≤3，等号在a＝b＝时成立．

    [解析]　由题意知A(2,0)，B(0,1)，所以线段AB的方程用截距式表示为＋y＝1，x∈[0,2]，又动点P(a，b)在线段AB上，所以＋b＝1，a∈[0,2]，又＋b≥2，所以1≥2，解得0≤ab≤，当且仅当＝b＝，即P(1，)时，ab取得最大值.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    幂指函数y=[f（x）]g（x）在求导时，可运用对数法：在函数解析式两边求对数得lny=g（x）•lnf（x），两边同时求导得
    y/
    y
    =g/(x)lnf(x)+g(x)
    f/(x)
    f(x)
    ，于是y′=[f(x)]g(x)[g/(x)lnf(x)+g(x)
    f/(x)
    f(x)
    ]    ，运用此方法可以探求得知y=x
    1
    x
    的一个单调递增区间为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某种商品一年内每件出厂价在7千元的基础上，按月呈f（x）=Asin（ωx+?）+B(A＞0，ω＞0，|φ|＜
    π
    2
    )    的模型波动（x为月份），已知3月份达到最高价9千元，7月份价格最低为5千元，根据以上条件可确定f（x）的解析式为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：013

    将函数y=f(x)的图像上每一点的横坐标变为原来的2倍，再将图像向左平移个单位，所得到的曲线的解析式是，那么函数y=f(x)的解析式是（　）

    A．　　　　　　　　　　　　　　　　　　  B．

    C．　　　　　　　　　　　　　　　　　　  D．

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：013

    将函数y=f(x)的图像上每一点的横坐标变为原来的2倍，再将图像向左平移个单位，所得到的曲线的解析式是，那么函数y=f(x)的解析式是（　）

    A．　　　　　　　　　　　　　　　　　　  B．

    C．　　　　　　　　　　　　　　　　　　  D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    过平行六面体ABCD－A1B1C1D1任意两条棱的中点作直线，其中与平面DBB1D1平行的直线共有(　　)

    A．4条          B．6条 

    C．8条          D．12条

    [答案]　D

    [解析]　如图所示，设M、N、P、Q为所在边的中点，

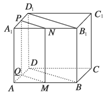
    则过这四个点中的任意两点的直线都与面DBB1D1平行，这种情形共有6条；同理，经过BC、CD、B1C1、C1D1四条棱的中点，也有6条；故共有12条，故选D.

    查看答案和解析>>

    同步练习册答案