
【题目】如图,正方体ABCD-A1B1C1D1的棱长为a , M为BD1的中点,N在A1C1上,且满足|A1N|=3|NC1|.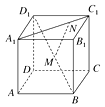
(1)求MN的长;
(2)试判断△MNC的形状.
【答案】
(1)解:以D为原点,建立空间直角坐标系,
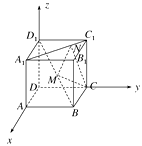
并设正方体边长为a,则B(a,a,0),D1(0,0,a),A1(a,0,a),C1(0,a,a),C(0,a,0),M( ![]() a,
a, ![]() a,
a, ![]() a),N(
a),N( ![]() a,
a, ![]() a,a),
a,a),
∴|MN|= ![]() =
= ![]() a.
a.
(2)解:∵ ![]() =(-
=(- ![]() a,
a, ![]() a,
a, ![]() a),
a), ![]() =(-
=(- ![]() a,
a, ![]() a,-
a,- ![]() a),
a), ![]() =(-
=(- ![]() a,
a, ![]() a,-a),
a,-a),
∴ ![]() ·
· ![]() =
= ![]() a2+
a2+ ![]() a2-
a2- ![]() a2=0,∴MN⊥MC,∴△MNC是直角三角形.
a2=0,∴MN⊥MC,∴△MNC是直角三角形.
【解析】本题根据题意可以选用坐标法来解题,根据向量的相关知识及空间线段长计算公式:![]() 及两向量数量积等于零得到两向量垂直,解出本题。
及两向量数量积等于零得到两向量垂直,解出本题。
【考点精析】关于本题考查的棱柱的结构特征,需要了解两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形才能得出正确答案.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】如图,在空间四边形ABCD中,E , F分别为AB , AD上的点,且 ![]() ,H , G分别为BC , CD的中点,则( )
,H , G分别为BC , CD的中点,则( )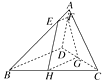
A.BD∥平面EFGH , 且四边形EFGH是平行四边形
B.EF∥平面BCD , 且四边形EFGH是梯形
C.HG∥平面ABD , 且四边形EFGH是平行四边形
D.EH∥平面ADC , 且四边形EFGH是梯形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用数学归纳法证明12+22+…+(n﹣1)2+n2+(n﹣1)2+…+22+12═ ![]() 时,由n=k的假设到证明n=k+1时,等式左边应添加的式子是( )
时,由n=k的假设到证明n=k+1时,等式左边应添加的式子是( )
A.(k+1)2+2k2
B.(k+1)2+k2
C.(k+1)2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi , yi)(i=1,2,…,n),用最小二乘法建立的回归方程为: ![]() =0.85x﹣85.71,则下列结论中不正确的是( )
=0.85x﹣85.71,则下列结论中不正确的是( )
A.3与3x2+2ax+b=0具有正的线性相关关系
B.回归直线过样本点的中心( ![]() ,
, ![]() )
)
C.若该大学某女生身高为170cm,则可断定其体重必为58.79kg
D.若该大学某女生身高增加1cm,则其体重约增加0.85kg
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.已知两组技工在单位时间内加工的合格零件平均数都为9.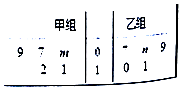
(1)分别求出m,n的值;
(2)分别求出甲、乙两组技工在单位时间内加工的合格零件的方差s甲2和s乙2 , 并由此分析两组技工的加工水平.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设y=f(x)是二次函数,方程f(x)=0有两个相等的实根,且f′(x)=2x﹣2.
(1)求y=f(x)的表达式;
(2)求y=f(x)的图象与两坐标轴所围成封闭图形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=ax2﹣2ax﹣1+b(a>0)在区间[2,3]上有最大值4和最小值1.设f(x)= ![]() .
.
(1)求a,b的值;
(2)若不等式f(2x)﹣k2x≥0在x∈[﹣1,1]上有解,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com