
【题目】在极坐标系中,直线l的极坐标方程为ρcosθ=4,曲线C的极坐标方程为ρ=2cosθ+2sinθ,以极点为坐标原点O,极轴为x轴的正半轴建立直角坐标系,射线l':y=kx(x≥0,0<k<1)与曲线C交于O,M两点.
(Ⅰ)写出直线l的直角坐标方程以及曲线C的参数方程;
(Ⅱ)若射线l′与直线l交于点N,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)直线l的直角坐标方程![]() ,曲线C的参数方程
,曲线C的参数方程![]() .
.
【解析】
(Ⅰ)由直线l的极坐标方程能求出直线l的直角坐标方程;由曲线C的极坐标方程,求出曲线C的直角坐标方程,由此能求出曲线C的参数方程.
(Ⅱ)用极径表示线段的长度,从而把比值问题转化为极坐标中极径的比值问题,再转化为以极角为变量的三角函数求范围问题.根据角的范围求即可.
解:(Ⅰ)∵直线l的极坐标方程为ρcos=4,
∴直线l的直角坐标方程为x=4,
∵曲线C的极坐标方程为ρ=2cosθ+2sinθ,
∴曲线C的直角坐标方程为x2+y2﹣2x﹣2y=0,即(x﹣1)2+(y﹣1)2=2.
∴曲线C的参数方程为![]() ,(α为参数).
,(α为参数).
(Ⅱ)设M(ρ1,β),N(ρ2,β),则ρ1=2cosβ+2sinβ,![]() ,
,
∴![]() =
=![]() =
=![]() =
=![]()
=![]() =
=![]() +
+![]()
![]() +
+![]() ,
,
∴![]()
![]() ,
,
∴![]() 的取值范围是(
的取值范围是(![]() ].
].


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2x+![]() )+cos(2x﹣
)+cos(2x﹣![]() )+cos2x﹣sin2x,x∈R.
)+cos2x﹣sin2x,x∈R.
(1)求函数f(x)的最小正周期及单调递增区间;
(2)求函数f(x)在区间[﹣![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面四边形MNPQ中,MN=![]() ,MP=1,MP⊥MN,PQ⊥QM.
,MP=1,MP⊥MN,PQ⊥QM.
(Ⅰ)若PQ=![]() ,求NQ的值;
,求NQ的值;
(Ⅱ)若∠MQN=30°,求sin∠QMP的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次演唱会上共10 名演员(每名演员都会唱歌或跳舞),其中7人能唱歌,6人会跳舞.
(1)问既能唱歌又会跳舞的有几人?
(2)现要选出一个2人唱歌2人伴舞的节目,有多少种选派方法?
查看答案和解析>>
科目:高中数学 来源: 题型:
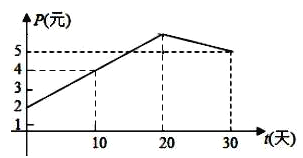
【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对![]() ,点
,点![]() 落在如图所示的两条线段上.该股票在30天内(包括30天)的日交易量M(万股)与时间t(天)的部分数据如下表所示:
落在如图所示的两条线段上.该股票在30天内(包括30天)的日交易量M(万股)与时间t(天)的部分数据如下表所示:
第t天 | 6 | 13 | 20 | 27 |
M(万股) | 34 | 27 | 20 | 13 |
(1)根据提供的图象,写出该股票每股交易价格P(元)与时间t(天)所满足的函数关系式![]() ______;
______;
(2)根据表中数据,写出日交易量M(万股)与时间t(天)的一次函数关系式:![]() ______;
______;
(3)用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求在这30天内第几天日交易额最大,最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
| 优秀 | 非优秀 | 总计 |
甲班 | 10 | ||
乙班 | 30 | ||
总计 | 105 |
已知在全部105人中随机抽取1人为优秀的概率为![]() .
.
(1)请完成上面的列联表;(把列联表自己画到答题卡上)
(2)根据列联表的数据,若按95%的可靠性要求,能否认为“成绩与班级有关系”?
参考公式:![]()
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 分别为椭圆
分别为椭圆![]() 的焦点,椭圆的右准线
的焦点,椭圆的右准线![]() 与
与![]() 轴交于
轴交于![]() 点,若
点,若![]() ,且
,且![]() .
.

(Ⅰ)求椭圆的方程;
(Ⅱ)过![]() 、
、![]() 作互相垂直的两直线分别与椭圆交于
作互相垂直的两直线分别与椭圆交于![]() 、
、![]() 、
、![]() 、
、![]() 四点,求四边形
四点,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定一个由![]() 个小正方形拼成的棋盘形方格,这些小正方形的颜色黑白相间(如图).
个小正方形拼成的棋盘形方格,这些小正方形的颜色黑白相间(如图).
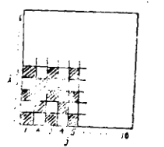
现定义一种运算A:把位于第i行的所有小正方形和位于第j列的所有小正方形都换成相反的颜色,即黑色的小正方形换成白色的,白色的小正方形换成黑色的,这里![]() .我们把A称为在位于第i行第j列上的小正方形上的一次运算.试问:能否经过若干次上述运算把棋盘上的所有小正方形全部换成同一种颜色?证明你的结论.
.我们把A称为在位于第i行第j列上的小正方形上的一次运算.试问:能否经过若干次上述运算把棋盘上的所有小正方形全部换成同一种颜色?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com