
【题目】已知点![]() 在椭圆
在椭圆![]() 内,过
内,过![]() 的直线
的直线![]() 与椭圆
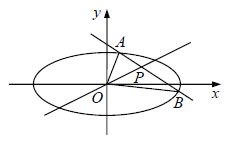
与椭圆![]() 相交于A,B两点,且点
相交于A,B两点,且点![]() 是线段AB的中点,O为坐标原点.
是线段AB的中点,O为坐标原点.
(Ⅰ)是否存在实数t,使直线![]() 和直线OP的倾斜角互补?若存在,求出
和直线OP的倾斜角互补?若存在,求出![]() 的值,若不存在,试说明理由;
的值,若不存在,试说明理由;
(Ⅱ)求![]() 面积S的最大值.
面积S的最大值.
【答案】( Ⅰ)存在;(Ⅱ) ![]() .
.
【解析】试题分析:
(Ⅰ)设出直线![]() 方程为
方程为![]() ,代入椭圆方程得关于
,代入椭圆方程得关于![]() 的一元二次方程,设
的一元二次方程,设![]() ,则可得
,则可得![]() ,利用
,利用![]() 可建立
可建立![]() 的关系,即
的关系,即![]() ,上面的一元二次方程有两个不等实根,即判别式
,上面的一元二次方程有两个不等实根,即判别式![]() ,由此可得
,由此可得![]() 的范围.注意特殊情形的讨论,最后由直线
的范围.注意特殊情形的讨论,最后由直线![]() 和直线
和直线![]() 的倾斜角互补,即斜率和为0可求得
的倾斜角互补,即斜率和为0可求得![]() ,若不能求出
,若不能求出![]() ,说明不存在);(Ⅱ)利用(Ⅰ)得直线
,说明不存在);(Ⅱ)利用(Ⅰ)得直线![]() 方程为
方程为![]() ,关键是由表示出
,关键是由表示出![]() ,
, ![]() ,这是
,这是![]() 的函数,可函数知识易求最值.
的函数,可函数知识易求最值.
试题解析:
(Ⅰ)存在.
由题意直线![]() 的斜率必存在,设直线
的斜率必存在,设直线![]() 的方程
的方程
是![]()
代入![]() 得:
得:
![]()
![]()
![]() .(1)
.(1)
设![]() ,
,![]() ,则
,则![]() ,即
,即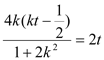 ,
,
解得:![]() ,
,
此时方程(1)即![]()
![]()
![]()
由![]() 解得,
解得,![]() ,
,
(或由![]() 解得,
解得,![]() )
)
当![]() 时,显然不符合题意;
时,显然不符合题意;
当![]() 时,设直线
时,设直线![]() 的斜率为
的斜率为![]() ,只需
,只需![]() ,
,
即![]() ,解得
,解得![]() ,均符合题意.
,均符合题意.
(Ⅱ)由(1)知![]() 的方程是
的方程是![]() ,
,
所以![]() ,
,
![]()
![]()
![]() ,
,
因为![]() ,所以当
,所以当![]() 时,
时,![]() .
.
点晴:解析几何中存在性问题的求解方法:
1.通常采用“肯定顺推法”,将不确定性问题明朗化,其步骤为:假设满足条件的元素(点、直线、曲线或参数)存在,用待定系数法设出,列出关于特定参数的方程组,若方程组有实数解,则元素(点、直线、曲线或参数)存在,否则(点、直线、曲线或参数)不存在.
2.反证法与验证法也是求解存在性问题的常用方法.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】中新网2016年12月19日电根据预报,今天开始雾霾范围将进一步扩大, ![]() 日夜间至
日夜间至![]() 日,雾霾严重时段部分地区
日,雾霾严重时段部分地区![]() 浓度峰值会超过
浓度峰值会超过![]() 微克/立方米. 而此轮雾霾最严重的时段,将有包括京津冀、山西、陕西、河南等
微克/立方米. 而此轮雾霾最严重的时段,将有包括京津冀、山西、陕西、河南等![]() 个省市在内的地区被雾霾笼罩.
个省市在内的地区被雾霾笼罩. ![]() 是指大气中直径小于或等于
是指大气中直径小于或等于![]() 微米的顆粒物,也称为可人肺颗粒物.
微米的顆粒物,也称为可人肺颗粒物. ![]() 日均值在
日均值在![]() 微克/立方米以下空气质量为一级;在
微克/立方米以下空气质量为一级;在![]() 微克/立方米
微克/立方米![]() 微克/立方米之间空气质量为二级;在
微克/立方米之间空气质量为二级;在![]() 微克/立方米以上空气质量为超标.某地区在2016年12月19日至28日每天的
微克/立方米以上空气质量为超标.某地区在2016年12月19日至28日每天的![]() 监测数据的茎叶图如下:
监测数据的茎叶图如下:

(1)求出这些数据的中位数与极差;
(2)从所给的空气质量不超标的![]() 天的数据中任意抽取
天的数据中任意抽取![]() 天的数据,求这
天的数据,求这![]() 天中恰好有
天中恰好有![]() 天空气质量为一级,另一天空气质量为二级的概率.
天空气质量为一级,另一天空气质量为二级的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数 ![]() 是定义在(﹣1,1)上的奇函数,且
是定义在(﹣1,1)上的奇函数,且 ![]() .
.
(1)确定函数的解析式;
(2)证明函数f(x)在(﹣1,1)上是增函数;
(3)解不等式f(t﹣1)+f(t)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),|
=(cosβ,sinβ),| ![]() ﹣
﹣ ![]() |=
|= ![]()
![]() .
.
(1)求cos(α﹣β)的值;
(2)若﹣ ![]() <β<0<α<
<β<0<α< ![]() ,且sinβ=﹣
,且sinβ=﹣ ![]() ,求sinα的值.
,求sinα的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinx+sin(x+ ![]() ),x∈R.
),x∈R.
(1)求f(x)的最小正周期;
(2)求f(x)的最大值和最小值;
(3)若f(α)= ![]() ,求sin 2α的值.
,求sin 2α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市统计局就某地居民的月收入调查了10 000人,并根据所得数据画出样本的频率分布直方图如图所示.(每个分组包括左端点,不包括右端点,如第一组表示[1 000,1 500)。

(1)求居民收入在[2000,3 000)的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这10 000人中按分层抽样方法抽出100人作进一步分析,则月收入在[2 000,3 000)的这段应抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直(其中
垂直(其中![]() 为自然对数的底数).
为自然对数的底数).
(I)求![]() 的解析式及单调递减区间;
的解析式及单调递减区间;
(II)是否存在常数![]() ,使得对于定义域内的任意
,使得对于定义域内的任意![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】.(本小题满分12分)
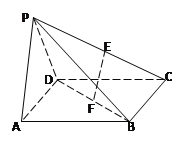
如图,四棱锥P—ABCD中,底面ABCD是边长为![]() 的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=![]() AD.
AD.
(Ⅰ)求证:EF//平面PAD;
(Ⅱ)求三棱锥C—PBD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 为公差不为
为公差不为![]() 的等差数列,
的等差数列, ![]() 为前
为前![]() 项和,
项和, ![]() 和
和![]() 的等差中项为
的等差中项为![]() ,且
,且![]() .令
.令![]() 数列
数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)求![]() 及
及![]() ;
;
(2)是否存在正整数![]() 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com