
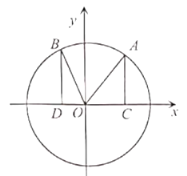
【题目】如图,在平面直角坐标系![]() 中,单位圆
中,单位圆![]() 上存在两点
上存在两点![]() ,满足
,满足![]() 均与
均与![]() 轴垂直,设
轴垂直,设![]() 与
与![]() 的面积之和记为
的面积之和记为![]() .
.
![]() 若
若![]() ,求
,求![]() 的值;
的值;
![]() 若对任意的
若对任意的![]() ,存在
,存在![]() ,使得
,使得![]() 成立,且实数
成立,且实数![]() 使得数列
使得数列![]() 为递增数列,其中
为递增数列,其中![]() 求实数
求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 或
或![]() (2)
(2)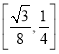
【解析】
(1)运用三角形的面积公式和三角函数的和差公式,以及特殊角的函数值,可得所求角;
(2)由正弦函数的值域可得![]() 的最大值,再由基本不等式可得
的最大值,再由基本不等式可得![]() 的最大值,可得
的最大值,可得![]() 的范围,再由数列的单调性,讨论
的范围,再由数列的单调性,讨论![]() 的范围,即可得到
的范围,即可得到![]() 的取值范围.
的取值范围.
![]() 依题意,可得
依题意,可得
![]()
![]()
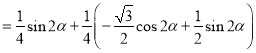
![]()
![]() ,
,
由![]() ,得
,得![]() ,
,
又![]() ,所以
,所以![]() .
.
![]() 由
由![]() 得
得![]()
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
当![]() 时,
时,![]() ,
,
(当且仅当![]() 时,等号成立)
时,等号成立)
又因为对任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,
成立,
所以![]() ,即
,即![]() ,解得
,解得![]() ,
,
因为数列![]() 为递增数列,且
为递增数列,且![]() ,
,
所以![]() ,从而
,从而![]() ,
,
又![]() ,所以
,所以![]() ,
,
从而![]() ,
,
又![]() ,
,
①当![]() 时,
时,![]() ,从而
,从而![]() ,
,
此时![]() 与
与![]() 同号,
同号,
又![]() ,即
,即![]() ,
,
②当![]() 时,由于
时,由于![]() 趋向于正无穷大时,
趋向于正无穷大时,![]() 与
与![]() 趋向于相等,从而
趋向于相等,从而![]() 与
与![]() 趋向于相等,即存在正整数
趋向于相等,即存在正整数![]() ,使
,使![]() ,从而
,从而![]() ,
,
此时![]() 与
与![]() 异号,与数列
异号,与数列![]() 为递增数列矛盾,
为递增数列矛盾,
综上,实数![]() 的取值范围为
的取值范围为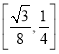 .
.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时,
时,![]() ,
,![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(Ⅲ)设曲线![]() ,点
,点![]() ,
,![]() 为该曲线上不同的两点.求证:当
为该曲线上不同的两点.求证:当![]() 时,直线
时,直线![]() 的斜率大于-1.
的斜率大于-1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() .
.
(1)求函数![]() 的最小正周期和对称轴方程;
的最小正周期和对称轴方程;
(2)若![]() ,求
,求![]() 的值域.
的值域.
【答案】(1)对称轴为![]() ,最小正周期
,最小正周期![]() ;(2)
;(2)![]()
【解析】
(1)利用正余弦的二倍角公式和辅助角公式将函数解析式进行化简得到![]() ,由周期公式和对称轴公式可得答案;(2)由x的范围得到
,由周期公式和对称轴公式可得答案;(2)由x的范围得到![]() ,由正弦函数的性质即可得到值域.
,由正弦函数的性质即可得到值域.
(1)![]()
![]()
令![]() ,则
,则
![]() 的对称轴为
的对称轴为![]() ,最小正周期
,最小正周期![]() ;
;
(2)当![]() 时,
时,![]() ,
,
因为![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
在![]() 取最大值,在
取最大值,在![]() 取最小值,
取最小值,
所以![]() ,
,
所以![]() .
.
【点睛】
本题考查正弦函数图像的性质,考查周期性,对称性,函数值域的求法,考查二倍角公式以及辅助角公式的应用,属于基础题.
【题型】解答题
【结束】
21
【题目】已知等比数列![]() 的前
的前![]() 项和为
项和为![]() ,公比
,公比![]() ,
,![]() ,
,![]() .
.
(1)求等比数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求
,求![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移1个单位长度,得到的图象是( )
A.
B.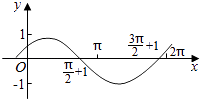
C.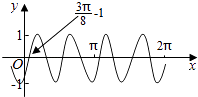
D.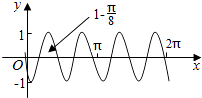
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村电费收取有以下两种方案供农户选择:
方案一:每户每月收取管理费2元,月用电量不超过30度时,每度0.5元;超过30度时,超过部分按每度0.6元收取;
方案二:不收管理费,每度0.58元.
(1)求方案一![]() 收费(元)与用电量
收费(元)与用电量![]() (度)间的函数关系;
(度)间的函数关系;
(2)老王家九月份按方案一交费35元,问老王家该月用电多少度?
(3)老王家该月用电量在什么范围内,选择方案一比选择方案二更好?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)对任意x,y∈R,总有f(x)+f(y)=f(x+y),且当x>0时,f(x)<0,f(1)=-![]() .
.
(1)求证:f(x)是R上的单调减函数.
(2)求f(x)在[-3,3]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2x+ ![]() )+sin(2x﹣
)+sin(2x﹣ ![]() )+2cos2x﹣1,x∈R.
)+2cos2x﹣1,x∈R.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间[ ![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com