
| A、若一条直线l与平面α平行,则直线l与平面α内所有直线平行 |
| B、若两条直线l1,l2都与平面α平行,则l1∥l2 |
| C、若一条直线与两个平面α,β都垂直,则平面α∥平面β |
| D、若一条直线与两个平面α,β都平行,则平面α∥平面β |


科目:高中数学 来源: 题型:
| A、20 | B、25 | C、28 | D、30 |
查看答案和解析>>
科目:高中数学 来源: 题型:
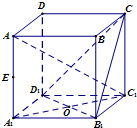 如图,在正方体ABCD-A1B1C1D1中,E是AA1的中点.
如图,在正方体ABCD-A1B1C1D1中,E是AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
| 甲高中 | 乙高中 | 丙高中 | |
| 女生 | 153 | x | y |
| 男生 | 97 | 90 | z |
| 8442 | 1753 | 3157 | 2455 | 0688 | 7704 | 7447 | 6721 | 7633 | 5026 | 8392 | |
| 6301 | 5316 | 5916 | 9275 | 3862 | 9821 | 5071 | 7512 | 8673 | 5807 | 4439 | |
| 1326 | 3321 | 1342 | 7864 | 1607 | 8252 | 0744 | 3815 | 0324 | 4299 | 7931 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| 3 |
| b |
| a |
| b |
| b |
| 1 |
| 2 |
| x |
| 2 |
| π |
| 3 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知圆E:(x+
如图,已知圆E:(x+| 3 |
| 3 |
| S1+S2 |
| S |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com