
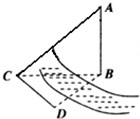
 如图,测量河对岸的旗杆高AB时,选与旗杆底B在同一水平面内的两个测点C与D,测得∠BCD=75°,∠BDC=60°,CD=a,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为
如图,测量河对岸的旗杆高AB时,选与旗杆底B在同一水平面内的两个测点C与D,测得∠BCD=75°,∠BDC=60°,CD=a,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为3
| ||
| 2 |
3
| ||
| 2 |
| BC |
| sin∠BDC |
| CD |
| sin∠CBD |
| CD•sin∠BDC |
| sin∠CBD |
| a•sin60° |
| sin45° |
| ||
| 2 |
| ||
| 2 |
3
| ||
| 2 |
3
| ||
| 2 |
3
| ||
| 2 |


科目:高中数学 来源: 题型:
 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个侧点C与D.现测得∠BCD=α,∠BDC=β,CD=s,并在点C测得塔顶A的仰角为θ,则塔高AB=
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个侧点C与D.现测得∠BCD=α,∠BDC=β,CD=s,并在点C测得塔顶A的仰角为θ,则塔高AB=| ssinβ |
| sin(α+β) |
| ssinβ |
| sin(α+β) |
查看答案和解析>>
科目:高中数学 来源:浙江省东阳市南马高中2010届高三上学期期中考试数学理科试题 题型:022
如图,测量河对岸的旗杆高AB时,选与旗杆底B在同一水平面内的两个测点C与D,测得∠BCD=75°,∠BDC=60°,CD=a,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为________.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山西省高三上学期第二次月考文科数学卷 题型:填空题
如右图,测量河对岸的旗杆高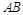 时,选与旗杆底
时,选与旗杆底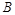 在同一水平面内的两个点
在同一水平面内的两个点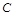 与
与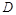 ,测得
,测得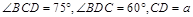 ,并在点
,并在点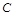 测得旗杆顶
测得旗杆顶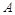 的仰角为
的仰角为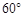 ,则旗杆高
,则旗杆高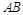 为 .
为 .

查看答案和解析>>
科目:高中数学 来源:浙江省东阳市南马高中2010届高三上学期期中考试(理) 题型:填空题
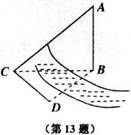 如图,测量河对岸的旗杆高
如图,测量河对岸的旗杆高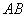 时,选与旗杆底
时,选与旗杆底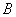 在
在
同一水平面内的两个测点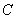 与
与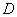 ,测得
,测得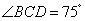 ,
,
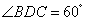 ,
, ,并在点
,并在点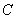 测得旗杆顶
测得旗杆顶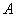 的
的
仰角为60°,则旗杆高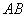 为
。
为
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com