
分析 利用指数函数与对数函数的单调性即可判断出.
解答 解:函数y=($\frac{1}{2}$)x,y=${log}_{\frac{1}{2}}$x.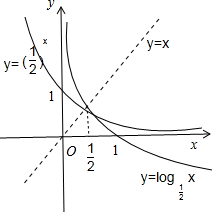
当$0<x≤\frac{1}{2}$时,$(\frac{1}{2})^{x}$∈$[\frac{\sqrt{2}}{2},1)$,$lo{g}_{\frac{1}{2}}x$≥1,因此a∉(0,$\frac{1}{2}$];
当$\frac{1}{2}<x<\frac{\sqrt{2}}{2}$时,$(\frac{1}{2})^{x}$∈$((\frac{1}{2})^{\frac{\sqrt{2}}{2}},\frac{\sqrt{2}}{2})$,$lo{g}_{\frac{1}{2}}x$∈$(\frac{1}{2},1)$,$\frac{1}{2}<(\frac{1}{2})^{\frac{\sqrt{2}}{2}}$,因此a∈$(\frac{1}{2},\frac{\sqrt{2}}{2})$;
当$\frac{\sqrt{2}}{2}≤x<1$时,$(\frac{1}{2})^{x}$∈$(\frac{1}{2},(\frac{1}{2})^{\frac{\sqrt{2}}{2}}]$,$lo{g}_{\frac{1}{2}}x$∈$(0,\frac{1}{2}]$,因此a∉∈[$\frac{\sqrt{2}}{2}$,1).
综上可得:a∈$(\frac{1}{2},\frac{\sqrt{2}}{2})$.
点评 本题考查了指数函数与对数函数的单调性,考查了推理能力与计算能力,属于中档题.


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com