
【题目】已知点A(﹣1,0),B(1,0),C(0,1),直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,则b的取值范围是( )
A.(0,1)B. C.
C. D.
D.![]()
【答案】B
【解析】
先求得直线y=ax+b(a>0)与x轴的交点为M(![]() ,0),由
,0),由![]() 0可得点M在射线OA上.求出直线和BC的交点N的坐标,①若点M和点A重合,求得b
0可得点M在射线OA上.求出直线和BC的交点N的坐标,①若点M和点A重合,求得b![]() ;②若点M在点O和点A之间,求得
;②若点M在点O和点A之间,求得![]() b
b![]() ; ③若点M在点A的左侧,求得
; ③若点M在点A的左侧,求得![]() b>1
b>1![]() .再把以上得到的三个b的范围取并集,可得结果.
.再把以上得到的三个b的范围取并集,可得结果.
由题意可得,三角形ABC的面积为 ![]() 1,
1,
由于直线y=ax+b(a>0)与x轴的交点为M(![]() ,0),
,0),
由直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,可得b>0,
故![]() 0,故点M在射线OA上.
0,故点M在射线OA上.
设直线y=ax+b和BC的交点为N,则由![]() 可得点N的坐标为(
可得点N的坐标为(![]() ,
,![]() ).
).
①若点M和点A重合,如图:

则点N为线段BC的中点,故N(![]() ,
,![]() ),
),
把A、N两点的坐标代入直线y=ax+b,求得a=b![]() .
.
②若点M在点O和点A之间,如图:
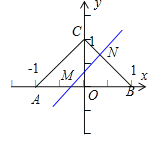
此时b![]() ,点N在点B和点C之间,
,点N在点B和点C之间,
由题意可得三角形NMB的面积等于![]() ,
,
即![]() ,即
,即 ![]() ,可得a
,可得a![]() 0,求得 b
0,求得 b![]() ,
,
故有![]() b
b![]() .
.
③若点M在点A的左侧,

则b![]() ,由点M的横坐标
,由点M的横坐标![]() 1,求得b>a.
1,求得b>a.
设直线y=ax+b和AC的交点为P,则由 ![]() 求得点P的坐标为(
求得点P的坐标为(![]() ,
,![]() ),
),
此时,由题意可得,三角形CPN的面积等于![]() ,即
,即 ![]() (1﹣b)|xN﹣xP|
(1﹣b)|xN﹣xP|![]() ,
,
即![]() (1﹣b)|
(1﹣b)|![]() |
|![]() ,化简可得2(1﹣b)2=|a2﹣1|.
,化简可得2(1﹣b)2=|a2﹣1|.
由于此时 b>a>0,0<a<1,∴2(1﹣b)2=|a2﹣1|=1﹣a2 .
两边开方可得 ![]() (1﹣b)
(1﹣b)![]() 1,∴1﹣b
1,∴1﹣b![]() ,化简可得 b>1
,化简可得 b>1![]() ,
,
故有1![]() b
b![]() .
.
综上可得b的取值范围应是  ,
,
故选:B.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,A1B1=A1C1 , D,E分别是棱BC,CC1上的点(点D 不同于点C),且AD⊥DE,F为B1C1的中点.求证: 
(1)平面ADE⊥平面BCC1B1;
(2)直线A1F∥平面ADE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列推理过程不是演绎推理的是( )
①一切奇数都不能被2整除,2019是奇数,2019不能被2整除;
②由“正方形面积为边长的平方”得到结论:正方体的体积为棱长的立方;
③在数列![]() 中,
中,![]() ,由此归纳出
,由此归纳出![]() 的通项公式;
的通项公式;
④由“三角形内角和为![]() ”得到结论:直角三角形内角和为
”得到结论:直角三角形内角和为![]() .
.
A. ①② B. ③④ C. ②③ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关线性回归分析的六个命题:
①线性回归直线必过样本数据的中心点![]() ;
;
②回归直线就是散点图中经过样本数据点最多的那条直线;
③当相关性系数![]() 时,两个变量正相关;
时,两个变量正相关;
④如果两个变量的相关性越强,则相关性系数![]() 就越接近于1;
就越接近于1;
⑤残差图中残差点所在的水平带状区域越宽,则回归方程的预报精确度越高;
⑥甲、乙两个模型的![]() 分别约为0.88和0.80,则模型乙的拟合效果更好.
分别约为0.88和0.80,则模型乙的拟合效果更好.
其中真命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E是CD的中点.
(1)证明:CD⊥平面PAE;
(2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P﹣ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xoy中,曲线C1上的点均在C2:(x﹣5)2+y2=9外,且对C1上任意一点M,M到直线x=﹣2的距离等于该点与圆C2上点的距离的最小值.
(1)求曲线C1的方程
(2)设P(x0 , y0)(y0≠±3)为圆C2外一点,过P作圆C2的两条切线,分别于曲线C1相交于点A,B和C,D.证明:当P在直线x=﹣4上运动时,四点A,B,C,D的纵坐标之积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业甲,乙两个研发小组,他们研发新产品成功的概率分别为![]() 和
和![]() ,现安排甲组研发新产品
,现安排甲组研发新产品![]() ,乙组研发新产品
,乙组研发新产品![]() .设甲,乙两组的研发是相互独立的.
.设甲,乙两组的研发是相互独立的.
(1)求至少有一种新产品研发成功的概率;
(2)若新产品![]() 研发成功,预计企业可获得
研发成功,预计企业可获得![]() 万元,若新产品
万元,若新产品![]() 研发成功,预计企业可获得利润
研发成功,预计企业可获得利润![]() 万元,求该企业可获得利润的分布列和数学期望.
万元,求该企业可获得利润的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com