
【题目】全网传播的融合指数是衡量电视媒体在中国网民中影响力的综合指标,根据相关报道提供的全网传播2018年某全国性大型活动的“省级卫视新闻台”融合指数的数据,对名列前20名的“省级卫视新闻台”的融合指数进行分组统计,结果如表所示.
组号 | 分组 | 频数 |
1 |
| 2 |
2 |
| 8 |
3 |
| 7 |
4 |
| 3 |
现从融合指数在![]() 和
和![]() 内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在
内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在![]() 内的概率.
内的概率.
【答案】![]() .
.
【解析】
方法一,设融合指数在![]() 内的“省级卫视新闻台”记为
内的“省级卫视新闻台”记为![]() ;融合指数在
;融合指数在![]() 内的“省级卫视新闻台”记为
内的“省级卫视新闻台”记为![]() ,列举所有的基本事件,并求满足条件的基本事件,按古典概型概率公式求概率.
,列举所有的基本事件,并求满足条件的基本事件,按古典概型概率公式求概率.
方法二,先求至少有1家的融合指数在![]() 内的对立事件的概率,再按对立事件公式求概率.
内的对立事件的概率,再按对立事件公式求概率.
方法一 融合指数在![]() 内的“省级卫视新闻台”记为
内的“省级卫视新闻台”记为![]() ;融合指数在
;融合指数在![]() 内的“省级卫视新闻台”记为
内的“省级卫视新闻台”记为![]() .
.
从融合指数在![]() 和
和![]() 内的“省级卫视新闻台”中随机抽取2家的所有可能结果为
内的“省级卫视新闻台”中随机抽取2家的所有可能结果为![]() ,
,![]() ,
,![]() ,共10个.
,共10个.
其中,至少有1家融合指数在![]() 内的所有可能结果为
内的所有可能结果为![]() ,
,![]() ,共9个,所以所求的概率
,共9个,所以所求的概率![]() .
.
方法二 融合指数在![]() 内的“省级卫视新闻台”记为
内的“省级卫视新闻台”记为![]() ,融合指数在
,融合指数在![]() 内的“省级卫视新闻台”记为
内的“省级卫视新闻台”记为![]() .
.
从融合指数在![]() 和
和![]() 内的“省级卫视新闻台”中随机抽取2家的所有可能结果是
内的“省级卫视新闻台”中随机抽取2家的所有可能结果是![]() ,
,![]() ,
,![]() ,共10个.
,共10个.
其中,没有1家融合指数在![]() 内的所有可能结果为
内的所有可能结果为![]() ,共1个,所以所求的概率
,共1个,所以所求的概率![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,当x>0时,![]() .
.
(1)求f(x)的解析式;
(2)设x∈[1,2]时,函数![]() ,是否存在实数m使得g(x)的最小值为6,若存在,求m的取值;若不存在,说明理由.
,是否存在实数m使得g(x)的最小值为6,若存在,求m的取值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人群中各种血型的人所占的比例见下表:
血腥 | A | B | AB | O |
该血型的人所占的比例/% | 28 | 29 | 8 | 35 |
已知同种血型的人可以互相输血,O型血可以给任一种血型的人输血,任何人的血都可以输给AB型血的人,其他不同血型的人不能互相输血.该人群中的小明是B型血,若他因病需要输血,问:
(1)任找一个人,其血可以输给小明的概率是多少?
(2)任找一个人,其血不能输给小明的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】各国医疗科研机构都在研制某种病毒疫苗,现有G,E,F三个独立的医疗科研机构,它们在一定时期内能研制出疫苗的概率分别是![]() .求:
.求:
(1)他们都研制出疫苗的概率;
(2)他们都失败的概率;
(3)他们能够研制出疫苗的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司在过去几年内使用某种型号的灯管1 000根,该公司对这些灯管的使用寿命(单位:h)进行了统计,统计结果如表所示:
分组 |
|
|
|
|
频数 | 48 | 121 | 208 | 223 |
频率 | ||||
分组 |
|
|
| |
频数 | 193 | 165 | 42 | |
频率 |
(1)将各组的频率填入表中;
(2)根据上述统计结果,估计该种型号灯管的使用寿命不足1500 h的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频数分布表和频率分布直方图,将使用手机时间不低于80分钟的学生称为“手机迷”.
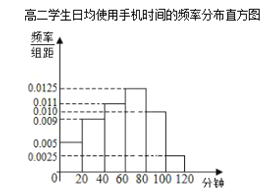
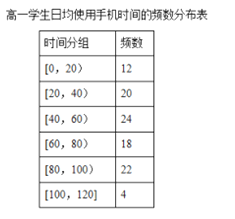
(I)将频率视为概率,估计哪个年级的学生是“手机迷”的概率大?请说明理由.
(II)在高二的抽查中,已知随机抽到的女生共有55名,其中10名为“手机迷”.根据已知条件完成下面的2×2列联表,并据此资料你有多大的把握认为“手机迷”与性别有关?
非手机迷 | 手机迷 | 合计 | |
男 | |||
女 | |||
合计 |
附:随机变量![]() (其中
(其中![]() 为样本总量).
为样本总量).
参考数据 |
| 0.15 | 0.10 | 0.05 | 0.025 |
| span>2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“开门大吉”是某电视台推出的游戏节目,选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁).其猜对歌曲名称与否的人数如图所示.
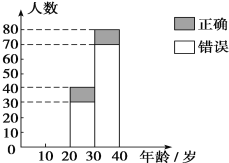
(1)写出2×2列联表;判断能否在犯错误的概率不超过0.10的前提下认为猜对歌曲名称与年龄有关系,说明你的理由.(下面的临界值表供参考)
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
(2)现计划在这次场外调查中按年龄段用分层抽样的方法选取6名选手,求20~30岁与30~40岁各有几人.
参考公式:K2=![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com