
【题目】在平面直角坐标系中,直线l的参数方程为![]() (t为参数,0).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数,0).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(Ⅰ)写出曲线C的直角坐标方程;
(Ⅱ)若直线l与曲线C交于A,B两点,且AB的长度为2![]() ,求直线l的普通方程.
,求直线l的普通方程.
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为![]() (t为参数),它与曲线C:(y-2)2-x2=1交于A、B两点.
(t为参数),它与曲线C:(y-2)2-x2=1交于A、B两点.
(1)求|AB|的长;
(2)以O为极点,x轴的正半轴为极轴建立极坐标系,设点P的极坐标为![]() ,求点P到线段AB中点M的距离.
,求点P到线段AB中点M的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为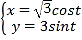 (t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程是
(t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程是![]() ,曲线
,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线l和曲线![]() 的直角坐标方程,曲线
的直角坐标方程,曲线![]() 的普通方程;
的普通方程;
(2)若直线l与曲线![]() 和曲线
和曲线![]() 在第一象限的交点分别为P,Q,求
在第一象限的交点分别为P,Q,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店销售某海鲜,统计了春节前后50天该海鲜的需求量![]() (
(![]() ,单位:公斤),其频率分布直方图如图所示,该海鲜每天进货1次,商店每销售1公斤可获利50元;若供大于求,剩余的削价处理,每处理1公斤亏损10元;若供不应求,可从其它商店调拨,销售1公斤可获利30元.假设商店每天该海鲜的进货量为14公斤,商店的日利润为
,单位:公斤),其频率分布直方图如图所示,该海鲜每天进货1次,商店每销售1公斤可获利50元;若供大于求,剩余的削价处理,每处理1公斤亏损10元;若供不应求,可从其它商店调拨,销售1公斤可获利30元.假设商店每天该海鲜的进货量为14公斤,商店的日利润为![]() 元.
元.

(1)求商店日利润![]() 关于需求量
关于需求量![]() 的函数表达式;
的函数表达式;
(2)假设同组中的每个数据用该组区间的中点值代替.
①求这50天商店销售该海鲜日利润的平均数;
②估计日利润在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】春节期间某商店出售某种海鲜礼盒,假设每天该礼盒的需求量在![]() 范围内等可能取值,该礼盒的进货量也在
范围内等可能取值,该礼盒的进货量也在![]() 范围内取值(每天进1次货).商店每销售1盒礼盒可获利50元;若供大于求,剩余的削价处理,每处理1盒礼盒亏损10元;若供不应求,可从其它商店调拨,销售1盒礼盒可获利30元.设该礼盒每天的需求量为
范围内取值(每天进1次货).商店每销售1盒礼盒可获利50元;若供大于求,剩余的削价处理,每处理1盒礼盒亏损10元;若供不应求,可从其它商店调拨,销售1盒礼盒可获利30元.设该礼盒每天的需求量为![]() 盒,进货量为
盒,进货量为![]() 盒,商店的日利润为
盒,商店的日利润为![]() 元.
元.
(1)求商店的日利润![]() 关于需求量
关于需求量![]() 的函数表达式;
的函数表达式;
(2)试计算进货量![]() 为多少时,商店日利润的期望值最大?并求出日利润期望值的最大值.
为多少时,商店日利润的期望值最大?并求出日利润期望值的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 满足:对任意实数
满足:对任意实数![]() ,方程
,方程![]() 的解的个数为偶数(可以是0个,但不能是无数个),则称
的解的个数为偶数(可以是0个,但不能是无数个),则称![]() 为“偶的函数”.证明:
为“偶的函数”.证明:
(1)任何多项式![]() 均不是偶的函数;
均不是偶的函数;
(2)存在连续函数![]() 是偶的函数.
是偶的函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )经过点
)经过点![]() ,且两个焦点
,且两个焦点![]() ,
,![]() 的坐标依次为
的坐标依次为![]() 和
和![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个动点,
上的两个动点,![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,若
,若![]() ,证明:直线
,证明:直线![]() 与以原点为圆心的定圆相切,并写出此定圆的标准方程.
与以原点为圆心的定圆相切,并写出此定圆的标准方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com