
【题目】如图,在四棱锥![]() 中,已知
中,已知![]() 是等边三角形,
是等边三角形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:
【题目】某中学利用周末组织教职员工进行了一次秋季登山健身的活动,有Ⅳ人参加,现将所有参加者按年龄情况分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 等七组,其频率分布直方图如图所示,已知
等七组,其频率分布直方图如图所示,已知![]() 这组的参加者是6人.
这组的参加者是6人.
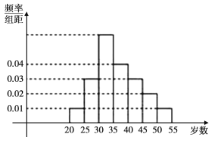
(1)已知![]() 和
和![]() 这两组各有2名数学教师,现从这两个组中各选取2人担任接待工作,设两组的选择互不影响,求两组选出的人中恰有1名数学老师的概率;
这两组各有2名数学教师,现从这两个组中各选取2人担任接待工作,设两组的选择互不影响,求两组选出的人中恰有1名数学老师的概率;
(2)组织者从![]() 这组的参加者(其中共有4名女教师,其余全为男教师)中随机选取3名担任后勤保障工作,其中女教师的人数为
这组的参加者(其中共有4名女教师,其余全为男教师)中随机选取3名担任后勤保障工作,其中女教师的人数为![]() ,求
,求![]() 的分布列和均值.
的分布列和均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》(第三季)亮点颇多,在“人生自有诗意”的主题下,十场比赛每场都有一首特别设计的开场诗词在声光舞美的配合下,百人团齐声朗诵,别有韵味.若《沁园春·长沙》、《蜀道难》、《敕勒歌》、《游子吟》、《关山月》、《清平乐·六盘山》排在后六场,且《蜀道难》排在《游子吟》的前面,《沁园春·长沙》与《清平乐·六盘山》不相邻且均不排在最后,则后六场的排法有__________种.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高一年级某个班分成7个小组,利用假期参加社会公益服务活动![]() 每个小组必须全员参加
每个小组必须全员参加![]() ,参加活动的次数记录如下:
,参加活动的次数记录如下:
组别 |
|
|
|
|
|
|
|
参加活动次数 | 3 | 2 | 4 | 3 | 3 | 4 | 2 |
![]() Ⅰ
Ⅰ![]() 求该班的7个小组参加社会公益服务活动数的中位数及与平均数v;
求该班的7个小组参加社会公益服务活动数的中位数及与平均数v;
![]() Ⅱ
Ⅱ![]() 从这7个小组中随机选出2个小组在全校进行活动汇报,求“选出的2个小组参加社会公益服务活动次数相等”的概率.
从这7个小组中随机选出2个小组在全校进行活动汇报,求“选出的2个小组参加社会公益服务活动次数相等”的概率.
![]() Ⅲ
Ⅲ![]() 至
至![]() 小组每组有4名同学,
小组每组有4名同学,![]() 小组有5名同学,记“该班学参加社会公益服务活动的平均次数”为
小组有5名同学,记“该班学参加社会公益服务活动的平均次数”为![]() ,写出
,写出![]() 与v的大小关系
与v的大小关系![]() 结论不要求证明
结论不要求证明![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的左焦点为
的左焦点为![]() ,且点
,且点![]() 在C上.
在C上.
![]() 求C的方程;
求C的方程;
![]() 设点P关于x轴的对称点为点
设点P关于x轴的对称点为点![]() 不经过P点且斜率为
不经过P点且斜率为![]() 的直线1与C交于A,B两点,直线PA,PB分别与x轴交于点M,N,求证:
的直线1与C交于A,B两点,直线PA,PB分别与x轴交于点M,N,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4 坐标系与参数方程选讲
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程
的参数方程 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 极坐标方程为
极坐标方程为![]() .
.
(1)求直线![]() 的普通方程以及曲线
的普通方程以及曲线![]() 的参数方程;
的参数方程;
(2)当![]() 时,
时,![]() 为曲线
为曲线![]() 上动点,求点
上动点,求点![]() 到直线
到直线![]() 距离的最大值.
距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下所示的列联表:
优秀 | 非优秀 | 总计 | |
甲班 | 10 |
| |
乙班 |
| 30 | |
总计 |
|
已知在全部105人中随机抽取1人,成绩优秀的概率为![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 列联表中![]() 的值为30,
的值为30,![]() 的值为35
的值为35
B. 列联表中![]() 的值为15,
的值为15,![]() 的值为50
的值为50
C. 根据列联表中的数据,若按![]() 的可靠性要求,能认为“成绩与班级有关系”
的可靠性要求,能认为“成绩与班级有关系”
D. 根据列联表中的数据,若按![]() 的可靠性要求,不能认为“成绩与班级有关系”
的可靠性要求,不能认为“成绩与班级有关系”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com