
【题目】已知函数f(x)=sin2 ![]() +
+ ![]() sinωx﹣
sinωx﹣ ![]() (ω>0),x∈R,若f(x)在区间(π,2π)内没有零点,则ω的取值范围是( )
(ω>0),x∈R,若f(x)在区间(π,2π)内没有零点,则ω的取值范围是( )
A.(0, ![]() ]
]
B.(0, ![]() ]∪[
]∪[ ![]() ,1)
,1)
C.(0, ![]() ]
]
D.(0, ![]() ]∪[
]∪[ ![]() ,
, ![]() ]
]
科目:高中数学 来源: 题型:
【题目】某研究小组在电脑上进行人工降雨模拟实验,准备用A、B、C三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其实验统计结果如下
方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验次数 |
A | 甲 | 2次 | 6次 | 4次 | 12次 |
B | 乙 | 3次 | 6次 | 3次 | 12次 |
C | 丙 | 2次 | 2次 | 8次 | 12次 |
假定对甲、乙、丙三地实施的人工降雨彼此互不影响,且不考虑洪涝灾害,请根据统计数据:
(1)求甲、乙、丙三地都恰为中雨的概率;
(2)考虑不同地区的干旱程度,当雨量达到理想状态时,能缓解旱情,若甲、丙地需中雨或大雨即达到理想状态,乙地必须是大雨才达到理想状态,记“甲、乙、丙三地中缓解旱情的个数”为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是正项数列
是正项数列![]() 的前
的前![]() 项和,且
项和,且![]() .
.
(Ⅰ)求数列![]() 通项公式;
通项公式;
(Ⅱ)是否存在等比数列![]() ,使
,使![]() 对一切正整数
对一切正整数![]() 都成立?并证明你的结论.
都成立?并证明你的结论.
(Ⅲ)设![]() (
(![]() ),且数列
),且数列![]() 的前
的前![]() 项和为
项和为![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】园林管理处拟在公园某区域规划建设一半径为![]() 米圆心角为
米圆心角为![]() (弧度)的扇形景观水池,其中
(弧度)的扇形景观水池,其中![]() 为扇形
为扇形![]() 的圆心,同时紧贴水池周边建一圈理想的无宽度步道,要求总预算费用不超过
的圆心,同时紧贴水池周边建一圈理想的无宽度步道,要求总预算费用不超过![]() 万元,水池造价为每平方米
万元,水池造价为每平方米![]() 元,步道造价为每米
元,步道造价为每米![]() 元.
元.
(1)当![]() 和
和![]() 分别为多少时,可使广场面积最大,并求出最大值;
分别为多少时,可使广场面积最大,并求出最大值;
(2)若要求步道长为![]() 米,则可设计出水池最大面积是多少.
米,则可设计出水池最大面积是多少.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知下列条件解三角形:
①A=60°,a= ![]() ,b=1;
,b=1;
②A=30°,a=1,b=2;
③A=30°,c=10,a=6;
④A=30°,c=10,a=5,
其中有唯一解的序号为( )
A.①②③
B.①②④
C.②③④
D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AD⊥AB,DC∥AB,PA=1,AB=2,PD=BC= ![]() .
. 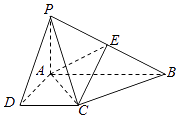
(1)求证:平面PAD⊥平面PCD;
(2)试在棱PB上确定一点E,使截面AEC把该几何体分成的两部分PDCEA与EACB的体积比为2:1;
(3)在(2)的条件下,求二面角E﹣AC﹣P的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com