
【题目】已知函数![]() 和
和![]() 在
在![]() 的图象如图所示:
的图象如图所示:
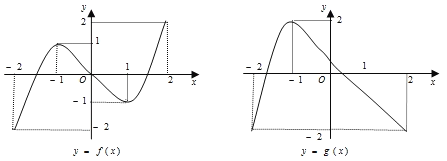
给出下列四个命题:
(1)方程![]() 有且仅有6个根;
有且仅有6个根;
(2)方程![]() 有且仅有3个根;
有且仅有3个根;
(3)方程![]() 有且仅有5个根;
有且仅有5个根;
(4)方程![]() 有且仅有4个根.
有且仅有4个根.
其中正确命题的个数是( )
A. 4个B. 3个C. 2个D. 1个
【答案】B
【解析】
把复合函数的定义域和值域进行对接,看满足外层函数为零时内层函数有几个自变量与之相对应.通过![]() 可知函数
可知函数![]() 有3个解,
有3个解,![]() 有2个解,然后具体分析①②③④,进而可得出正确的结论.
有2个解,然后具体分析①②③④,进而可得出正确的结论.
由图象可得![]() .
.
对于(1),由于满足方程![]() 的
的![]() 有三个不同值,一个值在2与1之间,一个值为0,一个值在1到2之间,由
有三个不同值,一个值在2与1之间,一个值为0,一个值在1到2之间,由![]() 的图象可得每个值
的图象可得每个值![]() 对应了2个
对应了2个![]() 值,故满足
值,故满足![]() 的
的![]() 值有6个,即方程
值有6个,即方程![]() 有且仅有6个根,故(1)正确.
有且仅有6个根,故(1)正确.
对于(2),由图可得满足![]() 的
的![]() 有两个,一个值处于2与1之间,由
有两个,一个值处于2与1之间,由![]() 的图象可得此时对应一个
的图象可得此时对应一个![]() 值;另一个值处于0与1之间,由
值;另一个值处于0与1之间,由![]() 的图象可得此时对应三个
的图象可得此时对应三个![]() 值,因此该方程有且仅有4个根.故(2)不正确.
值,因此该方程有且仅有4个根.故(2)不正确.
对于(3),由于满足方程![]() 的
的![]() 有3个不同的值,从图中可知一个
有3个不同的值,从图中可知一个![]() 等于0,一个
等于0,一个![]() ,一个
,一个![]() .而当
.而当![]() 对应了3个不同的
对应了3个不同的![]() 值;当
值;当![]() 时,只对应一个
时,只对应一个![]() 值;当
值;当![]() 时,也只对应一个
时,也只对应一个![]() 值.故满足方程
值.故满足方程![]() 的
的![]() 值共有5个,故(3)正确.
值共有5个,故(3)正确.
对于(4),由于满足方程![]() 的
的![]() 值有2个,而结合图象可得每个
值有2个,而结合图象可得每个![]() 值对应2个不同的
值对应2个不同的![]() 值,故满足方程
值,故满足方程![]() 的
的![]() 值有4个,即方程
值有4个,即方程![]() 有且仅有4个根,故(4)正确.
有且仅有4个根,故(4)正确.
综上得(1)(3)(4)正确.
故选B.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(Ⅰ)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列;
(Ⅱ)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程是 ![]() (θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,A、B的极坐标分别为A﹣(2,0)、B(﹣1,
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,A、B的极坐标分别为A﹣(2,0)、B(﹣1, ![]() )
)
(1)求直线AB的直角坐标方程;
(2)在曲线C上求一点M,使点M到AB的距离最大,并求出些最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
①圆![]() 与直线
与直线![]() 相交,所得弦长为
相交,所得弦长为![]() ;
;
②直线![]() 与圆
与圆![]() 恒有公共点;
恒有公共点;
③若棱长为![]() 的正方体的顶点都在同一球面上,则该球的表面积为
的正方体的顶点都在同一球面上,则该球的表面积为![]() ;
;
④若棱长为![]() 的正四面体的顶点都在同一球面上,则该球的体积为
的正四面体的顶点都在同一球面上,则该球的体积为![]() .
.
其中,正确命题的序号为__________.(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 同时满足:①对于定义域上的任意
同时满足:①对于定义域上的任意![]() ,恒有
,恒有![]() ;②对于定义域上的任意
;②对于定义域上的任意![]() .当
.当![]() ,恒有
,恒有![]() .则称函数
.则称函数![]() 为“理想函数”,则下列三个函数中:
为“理想函数”,则下列三个函数中:
(1)![]() ,
,
(2)![]() ,
,
(3)![]() .
.
称为“理想函数”的有 (填序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}共有5项,其中a1=0,a5=2,且|ai+1﹣ai|=1,i=1,2,3,4,则满足条件的不同数列的个数为( )
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数y=f(x),满足f(2)=0,函数y=f(x+1)的图象关于点(-1,0)中心对称,且对任意的负数x1,x2(x1≠x2),![]() 恒成立,则不等式f(x)<0的解集为____.
恒成立,则不等式f(x)<0的解集为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为R的函数f(x)满足:对于任意的实数x,y都有f(x+y)=f(x)+f(y)成立,且当x<0时,f(x)>0恒成立,且nf(x)=f(nx).(n是一个给定的正整数).
(1)判断函数f(x)的奇偶性,并证明你的结论;
(2)证明f(x)为减函数;若函数f(x)在[-2,5]上总有f(x)≤10成立,试确定f(1)应满足的条件;
(3)当a<0时,解关于x的不等式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究“晚上喝绿茶与失眠”有无关系,调查了100名人士,得到下面的列联表:
失眠 | 不失眠 | 合计 | |
晚上喝绿茶 | 16 | 40 | 56 |
晚上不喝绿茶 | 5 | 39 | 44 |
合计 | 21 | 79 | 100 |
由已知数据可以求得:![]() ,则根据下面临界值表:
,则根据下面临界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
可以做出的结论是( )
A. 在犯错误的概率不超过0.01的前提下认为“晚上喝绿茶与失眠有关”
B. 在犯错误的概率不超过0.01的前提下认为“晚上喝绿茶与失眠无关”
C. 在犯错误的概率不超过0.05的前提下认为“晚上喝绿茶与失眠有关”
D. 在犯错误的概率不超过0.05的前提下认为“晚上喝绿茶与失眠无关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com