
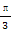 (ρ∈R). (2)ρcos2
(ρ∈R). (2)ρcos2 =1.
=1. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
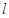 :
: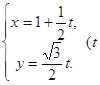 为参数), 曲线
为参数), 曲线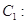
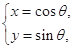 (
(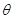 为参数).
为参数).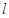 与
与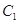 相交于
相交于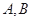 两点,求
两点,求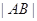 ;
;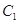 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的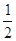 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的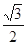 倍,得到曲线
倍,得到曲线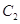 ,设点
,设点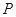 是曲线
是曲线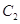 上的一个动点,求它到直线
上的一个动点,求它到直线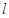 的距离的最小值.
的距离的最小值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
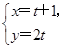 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为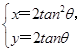 (θ为参数),试求直线l与曲线C的普通方程,并求出它们的公共点的坐标.
(θ为参数),试求直线l与曲线C的普通方程,并求出它们的公共点的坐标.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
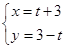 (参数t
(参数t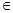 R).圆的参数方程为
R).圆的参数方程为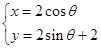 (参数
(参数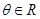 ),则圆C的圆心到直线l的距离为______.
),则圆C的圆心到直线l的距离为______.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
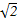 ρcos(θ-
ρcos(θ-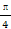 )=2.
)=2.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
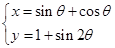 (θ为参数)有两个不同的交点,则实数a的取值范围为 .
(θ为参数)有两个不同的交点,则实数a的取值范围为 .查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
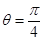 (
(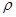 ∈R),它与曲线
∈R),它与曲线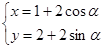 (
(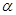 为参数)相交于两点A和B,则
为参数)相交于两点A和B,则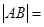 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com