
【题目】已知函数 ![]() .
.
(1)求f(x)的极值;
(2)当0<x<e时,求证:f(e+x)>f(e﹣x);
(3)设函数f(x)图象与直线y=m的两交点分别为A(x1 , f(x1)、B(x2 , f(x2)),中点横坐标为x0 , 证明:f'(x0)<0.
【答案】
(1)解:f′(x)= ![]() ,f(x)的定义域是(0,+∞),
,f(x)的定义域是(0,+∞),
x∈(0,e)时,f′(x)>0,f(x)单调递增;
x∈(e,+∞)时,f'(x)<0,f(x)单调递减.
当x=e时,f(x)取极大值为 ![]() ,无极小值
,无极小值
(2)解:要证f(e+x)>f(e﹣x),即证: ![]() ,
,
只需证明:(e﹣x)ln(e+x)>(e+x)ln(e﹣x).
设F(x)=(e﹣x)ln(e+x)﹣(e+x)ln(e﹣x),
![]() ,
,
∴F(x)>F(0)=0,
故(e﹣x)ln(e+x)>(e+x)ln(e﹣x),
即f(e+x)>f(e﹣x)
(3)解:证明:不妨设x1<x2,由(1)知0<x1<e<x2,∴0<e﹣x1<e,
由(2)得f[e+(e﹣x1)]>f[e﹣(e﹣x1)]=f(x1)=f(x2),
又2e﹣x1>e,x2>e,且f(x)在(e,+∞)上单调递减,
∴2e﹣x1<x2,即x1+x2>2e,
∴ ![]() ,∴f'(x0)<0
,∴f'(x0)<0
【解析】(1)求出函数的导数,解关于导函数的不等式,求出函数的极值即可;(2)问题转化为证明(e﹣x)ln(e+x)>(e+x)ln(e﹣x),设F(x)=(e﹣x)ln(e+x)﹣(e+x)ln(e﹣x),根据函数的单调性证明即可.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:吨)的影响,对近六年的年宣传费
(单位:吨)的影响,对近六年的年宣传费![]() 和年销售量
和年销售量![]() (
(![]() )的数据作了初步统计,得到如下数据:
)的数据作了初步统计,得到如下数据:
年份( | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年宣传费 | 23 | 25 | 27 | 29 | 32 | 35 |
年销售量 | 11 | 21 | 24 | 66 | 115 | 325 |
(1)根据散点图判断![]() 与
与![]() ,哪一个更适合作为年销售量
,哪一个更适合作为年销售量![]() (吨)与关于宣传费
(吨)与关于宣传费![]() (万元)的回归方程类型;
(万元)的回归方程类型;
(2)规定当产品的年销售量![]() (吨)与年宣传费
(吨)与年宣传费![]() (万元)的比值大于1时,认为该年效益良好,现从这6年中任选3年,记其中选到效益良好的数量为
(万元)的比值大于1时,认为该年效益良好,现从这6年中任选3年,记其中选到效益良好的数量为![]() ,试求
,试求![]() 的所有取值情况及对应的概率;
的所有取值情况及对应的概率;
(3)根据频率分布直方图中求出样本数据平均数的思想方法,求![]() 的平均数.
的平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线![]() 与圆
与圆 ![]() 且与椭圆
且与椭圆![]() 相交于
相交于![]() 两点.
两点.

(1)若直线![]() 恰好经过椭圆的左顶点,求弦长
恰好经过椭圆的左顶点,求弦长![]()
(2)设直线![]() 的斜率分别为
的斜率分别为![]() ,判断
,判断![]() 是否为定值,并说明理由
是否为定值,并说明理由
(3)求![]() ,面积的最小值.
,面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线C1的极坐标方程为ρ=4cosθ,直线l的参数方程为  (t为参数).
(t为参数).
(1)求曲线C1的直角坐标方程及直线l的普通方程;
(2)若曲线C2的参数方程为 ![]() (α为参数),曲线C1上点P的极角为
(α为参数),曲线C1上点P的极角为 ![]() ,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值.
,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线的顶点在坐标原点,焦点![]() 在
在![]() 轴正半轴上,过点
轴正半轴上,过点![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,线段
两点,线段![]() 的长是
的长是![]() ,
, ![]() 的中点到
的中点到![]() 轴的距离是
轴的距离是![]() .
.
(1)求抛物线的标准方程;
(2)过点![]() 作斜率为
作斜率为![]() 的直线与抛物线交于
的直线与抛物线交于![]() 两点,直线
两点,直线![]() 交抛物线于
交抛物线于![]() ,
,
①求证: ![]() 轴为
轴为![]() 的角平分线;
的角平分线;
②若![]() 交抛物线于
交抛物线于![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
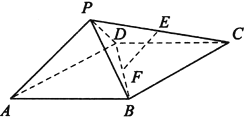
【题目】如图,四棱锥P—ABCD中,ABCD为矩形,△PAD为等腰直角三角形,
∠APD=90°,面PAD⊥面ABCD,且AB=1,AD=2,E、F分别为PC和BD的中点.
(1)证明:EF∥面PAD;
(2)证明:面PDC⊥面PAD;
(3)求四棱锥P—ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,点A的极坐标为(3, ![]() ),点B的极坐标为(6,
),点B的极坐标为(6, ![]() ),曲线C:(x﹣1)2+y2=1
),曲线C:(x﹣1)2+y2=1
(1)求曲线C和直线AB的极坐标方程;
(2)过点O的射线l交曲线C于M点,交直线AB于N点,若|OM||ON|=2,求射线l所在直线的直角坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com