
【题目】如图,在长方体![]() 中,点
中,点![]() 分别是棱
分别是棱![]() ,
,![]() 上的动点,
上的动点,![]() ,直线
,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则△
,则△![]() 的面积的最小值是________.
的面积的最小值是________.
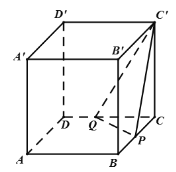
【答案】8
【解析】
以C为原点,CD,CB,CC′为坐标轴建立空间直角坐标系,设P(0,a,0),Q(b,0,0),求出平面PQC′的法向量![]() ,则由
,则由![]() 解出a,b的关系式,利用基本不等式得出
解出a,b的关系式,利用基本不等式得出![]() 的面积的最小值,再利用等体积法求出△
的面积的最小值,再利用等体积法求出△![]() 的面积的最小值.
的面积的最小值.
以C为原点,CD,CB,CC′为坐标轴建立空间直角坐标系,如图所示:
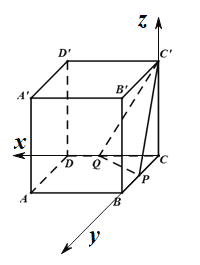
则C(0,0,0),![]() 设P(0,a,0),Q(b,0,0),于是0<a≤4,0<b≤3.
设P(0,a,0),Q(b,0,0),于是0<a≤4,0<b≤3.![]()
设平面PQC′的一个法向量为![]() 则
则
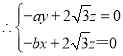 ,令z=1,得
,令z=1,得
![]()
 ,
,
![]() ,解得ab≥8(当且仅当
,解得ab≥8(当且仅当![]() 时等号成立),
时等号成立),
∴当ab=8时,S△PQC=4,棱锥C′-PQC的体积最小,
∵直线CC′与平面PQC′所成的角为30°,∴C到平面PQC′的距离d=2![]()
∵VC′-PQC=VC-PQC′,![]() .
.


科目:高中数学 来源: 题型:
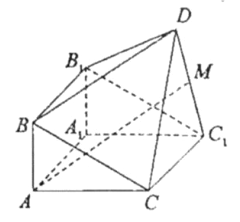
【题目】如图,由直三棱柱![]() 和四棱锥
和四棱锥![]() 构成的几何体中,
构成的几何体中,![]() ,平面
,平面![]() 平面
平面![]()
(I)求证:![]() ;
;
(II)若M为![]() 中点,求证:
中点,求证:![]() 平面
平面![]() ;
;
(III)在线段BC上(含端点)是否存在点P,使直线DP与平面![]() 所成的角为
所成的角为![]() ?若存在,求
?若存在,求![]() 得值,若不存在,说明理由.
得值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生产企业研发了一种新产品,该新产品在某网店试销一个阶段后得到销售单价![]() 和月销售量
和月销售量![]() 之间的一组数据,如下表所示:
之间的一组数据,如下表所示:
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 |
月销售量 | 11 | 10 | 8 | 6 | 5 |
(I)根据统计数据,求出![]() 关于
关于![]() 的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
(II)生产企业与网店约定:若该新产品的月销售量不低于10万件,则生产企业奖励网店1万元;若月销售量不低于8万件且不足10万件,则生产企业奖励网店5000元;若月销售量低于8万件,则没有奖励. 现用样本估计总体,从上述5个销售单价中任选2个销售单价,求抽到的产品含有月销售量不低于10万件的概率.
参考公式:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为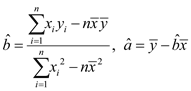 . 参考数据:
. 参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为![]()

(1)求频率分布直方图中![]() 的值;
的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在![]() 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}的前n项和为Sn,a2+a15=17,S10=55.数列{bn}满足an=log2bn.
(1)求数列{bn}的通项公式;
(2)若数列{an+bn}的前n项和Tn满足Tn=S32+18,求n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某音乐院校举行“校园之星”评选活动,评委由本校全体学生组成,对![]() 两位选手,随机调查了
两位选手,随机调查了![]() 个学生的评分,得到下面的茎叶图:
个学生的评分,得到下面的茎叶图:
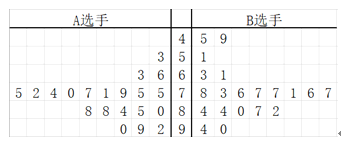
![]() 通过茎叶图比较
通过茎叶图比较![]() 两位选手所得分数的平均值及分散程度(不要求计算出具体值,得出结论即可);
两位选手所得分数的平均值及分散程度(不要求计算出具体值,得出结论即可);
![]() 校方将会根据评分记过对参赛选手进行三向分流:
校方将会根据评分记过对参赛选手进行三向分流:
所得分数 | 低于 |
| 不低于 |
分流方向 | 淘汰出局 | 复赛待选 | 直接晋级 |
记事件![]() “
“![]() 获得的分流等级高于
获得的分流等级高于![]() ”,根据所给数据,以事件发生的频率作为相应事件发生的概率,求事件
”,根据所给数据,以事件发生的频率作为相应事件发生的概率,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其导函数为
,其导函数为![]() .
.
(1)当![]() ,求
,求![]() 图象在
图象在![]() 处的切线方程;
处的切线方程;
(2)设![]() 在定义域上是单调函数,求
在定义域上是单调函数,求![]() 得取值范围;
得取值范围;
(3)若![]() 的极大值和极小值分别为
的极大值和极小值分别为![]() 、
、![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com