练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数
    （1）判断函数 的奇偶性.
    （2）求 的值域.

    【答案】
    （1）解： 的定义域为R，
    是奇函数.
    （2）解： ，∵
    ， ，
    的值域为 .
    【解析】本题主要考查函数的性质奇偶性和函数值域的求法。（1）主要利用奇偶性的定义来判断。（2）求函数值域的方法有很多，本题主要考查用分离常数的方法进行求解。
    【考点精析】本题主要考查了函数的值域和函数的奇偶性的相关知识点，需要掌握求函数值域的方法和求函数最值的常用方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的；偶函数的图象关于y轴对称；奇函数的图象关于原点对称才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数 .
    （1）讨论 的单调性；
    （2）若 有两个极值点 ， ，证明： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线 的焦点为F,直线 与x轴的交点为P,与抛物线的交点为Q,且 .
    （1）求抛物线的方程;
    （2）过F的直线l与抛物线相交于A,D两点,与圆 相交于B,C两点(A,B两点相邻),过A,D两点分别作抛物线的切线,两条切线相交于点M,求△ABM与△CDM的面积之积的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】执行如图所示的程序框图，若输出的结果是8，则判断框内m的取值范围是（ ）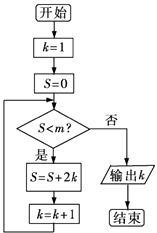
    A.（30，42]
    B.（42，56]
    C.（56，72]
    D.（30，72）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】集合U＝R，A＝{x|x2－x－2<0}，B＝{x|y＝ln(1－x)}，则图中阴影部分所表示的集合是( )

    A.{x|x≥1}
    B.{x|1≤x<2}
    C.{x|0<x≤1}
    D.{x|x≤1}

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数 的定义域为 ，如果 ， ，使 （ 为常数）成立，则称函数 在 上的均值为 ．给出下列四个函数：① ；② ；③ ；④ ．则其中满足在其定义域上均值为2的函数是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)=sin(cosx)-x与函数g(x)=cos(sinx)-x在区间(0， )都为减函数，设x1,x2,x3∈(0， )，且cosx1=x1 ， sin(cosx2)=x2 ， cos(sinx3)=x3 ， 则x1,x2,x3的大小关系是（ ）
    A.x1<x2<x3
    B.x3<x1<x2
    C.x2<x1<x3
    D.x2<x3<x1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分12分）已知函数，( 为常数)．

    （1）求函数在点 (，)处的切线方程；

    （2）当时，设，若函数在定义域上存在单调减区间，求实数的取值范围；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设锐角三角形的内角的对边分别为， ．

    （Ⅰ）求的大小；

    （Ⅱ）求的取值范围．

    查看答案和解析>>

    同步练习册答案