解:(1)当a=0时,f(x)=x
3-3x
2-9x,f'(x)=3x
2-6x-9=3(x+1)(x-3),列表如下:
| x | … | (-∞,-1) | -1 | (-1,3) | 3 | (3,+∞) | … |
| f'(x) | … | + | 0 | - | 0 | + | … |
| f (x) | … | ↗ | 极大值 | ↘ | 极小值 | ↗ | … |
所以f(x)的极大值为f(-1)=5,极小值为f(3)=-27. …(4分)
(2)令 g(x)=x
2-3(1-a)x+a
2+8a-9,则问题等价于当x>0时,g(x)=x
2-3(1-a)x+a
2+8a-9≥0,求a的取值范围.
ⅰ)若二次函数g(x)的对称轴
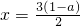
<0,即a>1时,根据图象,只需g(0)≥0,即a
2+8a-9≥0,解得a≤-9或a≥1,结合a>1,得a>1.
ⅱ)若二次函数g(x)的对称轴
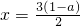
≥0,即a≤1时,根据图象,只需△=9(1-a)2-4(a2+8a-9)≤0,解得1≤a≤9.结合a≤1,得a=1.
故当x>0时,f(x)≥0,实数a的取值范围是a≥1. …(9分)
(3)要使函数f(x)在(0,1)上是减函数,只需f′(x)在(0,1)上恒小于0,因为 f'(x)=3x
2-6(1-a)x+a
2+8a-9,其二次项系数为3,从而只需f(0)≤0,且 f(1)≤0,
即
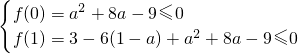
,解得
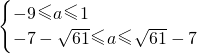
∵
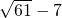
<1,所以-9≤a≤
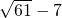
.
综上所述,若函数f(x)在(0,1)上是减函数,则a的取值范围是-9≤a≤
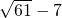
.…(14分)
分析:(1)当a=0时,求导数,确定函数的单调性,即可得到函数f(x)的极大值、极小值;
(2)令g(x)=x
2-3(1-a)x+a
2+8a-9,则问题等价于当x>0时,g(x)=x
2-3(1-a)x+a
2+8a-9≥0,求a的取值范围.利用函数的对称轴,分类讨论,即可求实数a的取值范围;
(3)要使函数f(x)在(0,1)上是减函数,只需f′(x)在(0,1)上恒小于0,因为 f'(x)=3x
2-6(1-a)x+a
2+8a-9,其二次项系数为3,从而只需f(0)≤0,且 f(1)≤0,由此可得a的取值范围.
点评:本题考查导数知识的运用,考查函数的单调性与极值,考查恒成立问题,正确求导是关键.

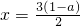 <0,即a>1时,根据图象,只需g(0)≥0,即a2+8a-9≥0,解得a≤-9或a≥1,结合a>1,得a>1.
<0,即a>1时,根据图象,只需g(0)≥0,即a2+8a-9≥0,解得a≤-9或a≥1,结合a>1,得a>1.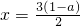 ≥0,即a≤1时,根据图象,只需△=9(1-a)2-4(a2+8a-9)≤0,解得1≤a≤9.结合a≤1,得a=1.
≥0,即a≤1时,根据图象,只需△=9(1-a)2-4(a2+8a-9)≤0,解得1≤a≤9.结合a≤1,得a=1.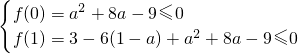 ,解得
,解得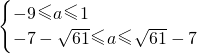
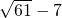 <1,所以-9≤a≤
<1,所以-9≤a≤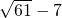 .
.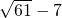 .…(14分)
.…(14分)
