
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() ,当
,当![]() 最大时,求出直线
最大时,求出直线![]() 的直角坐标方程.
的直角坐标方程.
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】德国数学家莱布尼兹(1646年-1716年)于1674年得到了第一个关于π的级数展开式,该公式于明朝初年传入我国.在我国科技水平业已落后的情况下,我国数学家天文学家明安图(1692年-1765年)为提高我国的数学研究水平,从乾隆初年(1736年)开始,历时近30年,证明了包括这个公式在内的三个公式,同时求得了展开三角函数和反三角函数的6个新级数公式,著有《割圆密率捷法》一书,为我国用级数计算π开创了先河.如图所示的程序框图可以用莱布尼兹“关于π的级数展开式”计算π的近似值(其中P表示π的近似值),若输入![]() ,则输出的结果是( )
,则输出的结果是( )
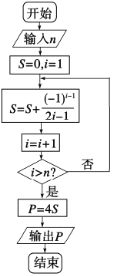
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修 4-4]参数方程与极坐标系
在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() :
: ![]() ,以平面直角坐标系
,以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,取相同的单位长度建立极坐标系.已知直线
轴正半轴为极轴,取相同的单位长度建立极坐标系.已知直线 ![]() :
: ![]() .
.
(Ⅰ)试写出直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的参数方程;
的参数方程;
(Ⅱ)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
[选修 4-5]不等式选讲
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产的产品中分正品与次品,正品重![]() ,次品重
,次品重![]() ,现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品)如果将5袋产品以1~5编号,第
,现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品)如果将5袋产品以1~5编号,第![]() 袋取出
袋取出![]() 个产品(
个产品(![]() ),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量
),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量![]() ,若次品所在的袋子的编号是2,此时的重量
,若次品所在的袋子的编号是2,此时的重量![]() _________
_________![]() ;若次品所在的袋子的编号是
;若次品所在的袋子的编号是![]() ,此时的重量
,此时的重量![]() _______
_______![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(13分)编号为A1,A2,…,A16的16名篮球运动员在某次训练比赛中的得分记录如下:
运动员编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | |
得分 | 15 | 35 | 21 | 28 | 25 | 36 | 18 | 34 | |
运动员编号 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 | |
得分 | 17 | 26 | 25 | 33 | 22 | 12 | 31 | 38 |
(Ⅰ)将得分在对应区间内的人数填入相应的空格;
区间 | [10,20) | [20,30) | [30,40] |
人数 |
(Ⅱ)从得分在区间[20,30)内的运动员中随机抽取2人,
(i)用运动员的编号列出所有可能的抽取结果;
(ii)求这2人得分之和大于50分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】奇函数f(x)在R上存在导数![]() ,当x<0时,
,当x<0时,![]()
![]() f(x),则使得(x2﹣1)f(x)<0成立的x的取值范围为( )
f(x),则使得(x2﹣1)f(x)<0成立的x的取值范围为( )
A.(﹣1,0)∪(0,1)B.(﹣∞,﹣1)∪(0,1)
C.(﹣1,0)∪(1,+∞)D.(﹣∞,﹣1)∪(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆周率是圆的周长与直径的比值,一般用希腊字母![]() 表示.早在公元480年左右,南北朝时期的数学家祖冲之就得出精确到小数点后7位的结果,他是世界上第一个把圆周率的数值计算到小数点后第7位的人,这比欧洲早了约1000年.生活中,我们也可以通过如下随机模拟试验来估计
表示.早在公元480年左右,南北朝时期的数学家祖冲之就得出精确到小数点后7位的结果,他是世界上第一个把圆周率的数值计算到小数点后第7位的人,这比欧洲早了约1000年.生活中,我们也可以通过如下随机模拟试验来估计![]() 的值:在区间
的值:在区间![]() 内随机取
内随机取![]() 个数,构成
个数,构成![]() 个数对
个数对![]() ,设
,设![]() ,
,![]() 能与1构成钝角三角形三边的数对
能与1构成钝角三角形三边的数对![]() 有
有![]() 对,则通过随机模拟的方法得到的
对,则通过随机模拟的方法得到的![]() 的近似值为( )
的近似值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求函数
垂直,求函数![]() 在
在![]() 点处的切线方程;
点处的切线方程;
(2)若对于![]() ,
,![]() 恒成立,求正实数
恒成立,求正实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,且函数
,且函数![]() 有极大值点
有极大值点![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com