
【题目】若关于x的不等式![]() 的解集为
的解集为![]() , 且函数
, 且函数![]() 在区间
在区间![]() 上不是单调函数,则实数m的取值范围为 ( )
上不是单调函数,则实数m的取值范围为 ( )
A.![]()
B.![]()
C.![]()
D.![]()
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣6x2+9x,g(x)= ![]() x3﹣
x3﹣ ![]() x2+ax﹣
x2+ax﹣ ![]() (a>1)若对任意的x1∈[0,4],总存在x2∈[0,4],使得f(x1)=g(x2),则实数a的取值范围为( )
(a>1)若对任意的x1∈[0,4],总存在x2∈[0,4],使得f(x1)=g(x2),则实数a的取值范围为( )
A.(1, ![]() ]
]
B.[9,+∞)??
C.(1, ![]() ]∪[9,+∞)
]∪[9,+∞)
D.[ ![]() ,
, ![]() ]∪[9,+∞)
]∪[9,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市公租房的房源位于A,B,C,D四个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,在该市的甲、乙、丙三位申请人中:
(1)求恰有1人申请A片区房源的概率;
(2)用x表示选择A片区的人数,求x的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={a1 , a2 , …,an},ai∈R,i=1,2,…,n,并且n≥2. 定义 ![]() (例如:
(例如: ![]() ).
).
(Ⅰ)若A={1,2,3,4,5,6,7,8,9,10},M={1,2,3,4,5},集合A的子集N满足:N≠M,且T(M)=T(N),求出一个符合条件的N;
(Ⅱ)对于任意给定的常数C以及给定的集合A={a1 , a2 , …,an},求证:存在集合B={b1 , b2 , …,bn},使得T(B)=T(A),且 ![]() .
.
(Ⅲ)已知集合A={a1 , a2 , …,a2m}满足:ai<ai+1 , i=1,2,…,2m﹣1,m≥2,a1=a,a2m=b,其中a,b∈R为给定的常数,求T(A)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等腰三角形ABC,E为底边BC的中点,沿AE折叠,如图,将C折到点P的位置,使P﹣AE﹣C为120°,设点P在面ABE上的射影为H. 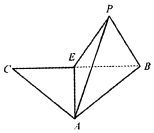
(1)证明:点H为EB的中点;
(2)若 ![]() ,求直线BE与平面ABP所成角的正弦值.
,求直线BE与平面ABP所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数x、y满足  ,目标函数z=x+ay.
,目标函数z=x+ay.
(1)当a=﹣2时,求目标函数z的取值范围;
(2)若使目标函数取得最小值的最优解有无数个,求 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在各项均为正数的等比数列{an}中,a1=2,且2a1 , a3 , 3a2成等差数列.
(Ⅰ) 求等比数列{an}的通项公式;
(Ⅱ) 若数列{bn}满足bn=11﹣2log2an , 求数列{bn}的前n项和Tn的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( ) 
A.f(x)=x2
B.f(x)= ![]()
C.f(x)=ex
D.f(x)=sinx
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos4x+sin2x,下列结论中错误的是( )
A.f(x)是偶函数
B.函f(x)最小值为 ![]()
C.![]() 是函f(x)的一个周期
是函f(x)的一个周期
D.函f(x)在(0, ![]() )内是减函数
)内是减函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com