
分析 (Ⅰ) 根据勾股定理,建立方程,进而求得动圆圆心的轨迹C的方程;
(Ⅱ)设P(x1,y1),Q(x2,y2),由题意,直线PQ的方程代入化简,利用角平分线的性质可得kPB=-kQB,可化为:-16tm+(3+m)8t=0,所以:m=3,l:x=ty+3,即可得到定点.
解答 解:(Ⅰ)设动圆圆心P(x,y),则|PM|2=|PA|2=42+x2即:(x-4)2+y2=42+x2,
即动圆圆心的轨迹方程为:y2=8x,
(Ⅱ) 设两点P(x1,y1),Q(x2,y2)设不垂直于x轴的直线:l:x=ty+m(t≠0),则$\left\{{\begin{array}{l}{x=ty+m}\\{{y^2}=8x}\end{array}}\right.$有:y2-8ty-8m=0,所以:y1+y2=8t,y1y2=-8m,
因为x轴是∠PBQ的角平分线,
所以:kBP+kBQ=0即:$\frac{y_1}{{{x_1}+3}}+\frac{y_2}{{{x_2}+3}}=0$即:2ty1y2+(m+3)(y1+y2)=0,
则:-16tm+(3+m)8t=0,所以:m=3l:x=ty+3所以直线l过定点(3,0).
点评 本题综合考查了抛物线的标准方程、直线与抛物线相交问题、直线方程及过定点问题、斜率计算公式等基础知识,考查了推理能力、数形结合的思想方法、计算能力、分析问题和解决问题的能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 偶函数 | B. | 奇函数 | ||
| C. | 定义域上的增函数 | D. | 定义域上的减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 1 | C. | -1 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A={0,1,2} | B. | {-2} | C. | {-1,0,1} | D. | {-2,-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 离心率相等 | B. | 虚半轴长相等 | C. | 实半轴长相等 | D. | 焦距相等 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
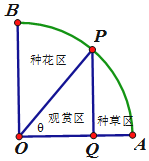 如图,一个圆心角为直角的扇形AOB 花草房,半径为1,点P 是花草房弧上一个动点,不含端点,现打算在扇形BOP 内种花,PQ⊥OA,垂足为Q,PQ 将扇形AOP
如图,一个圆心角为直角的扇形AOB 花草房,半径为1,点P 是花草房弧上一个动点,不含端点,现打算在扇形BOP 内种花,PQ⊥OA,垂足为Q,PQ 将扇形AOP 查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com