
【题目】已知在极坐系中,点![]() 绕极点
绕极点![]() 顺时针旋转角
顺时针旋转角![]() 得到点
得到点![]() .以
.以![]() 为原点,极轴为
为原点,极轴为![]() 轴非负半轴,并取相同的单位长度建立平面直角坐标系,曲线
轴非负半轴,并取相同的单位长度建立平面直角坐标系,曲线![]() 绕
绕![]() 逆时针旋转
逆时针旋转![]() 得到曲线
得到曲线![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 过点
过点![]() 且与曲线
且与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的最小值.
的最小值.
科目:高中数学 来源: 题型:
【题目】某乡镇响应“绿水青山就是金山银山”的号召,因地制宜的将该镇打造成“生态水果特色小镇”.经调研发现:某珍稀水果树的单株产量![]() (单位:千克)与施用肥料
(单位:千克)与施用肥料![]() (单位:千克)满足如下关系:
(单位:千克)满足如下关系: ,肥料成本投入为
,肥料成本投入为![]() 元,其它成本投入(如培育管理、施肥等人工费)
元,其它成本投入(如培育管理、施肥等人工费)![]() 元.已知这种水果的市场售价大约为15元/千克,且销路畅通供不应求.记该水果树的单株利润为
元.已知这种水果的市场售价大约为15元/千克,且销路畅通供不应求.记该水果树的单株利润为![]() (单位:元).
(单位:元).
(Ⅰ)求![]() 的函数关系式;
的函数关系式;
(Ⅱ)当施用肥料为多少千克时,该水果树的单株利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,AB⊥侧面BCC1B1,AC=AB1.
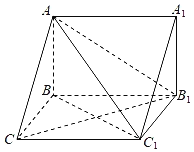
(1)求证:平面ABC1⊥平面AB1C;
(2)若AB=BC=2,∠BCC1=60°,求二面角B﹣AC1﹣B1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为正项数列
为正项数列![]() 的前
的前![]() 项和,满足
项和,满足![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)若不等式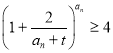 对任意正整数
对任意正整数![]() 都成立,求实数
都成立,求实数![]() 的取值范围;
的取值范围;
(3)设![]() (其中
(其中![]() 是自然对数的底数),求证:
是自然对数的底数),求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,PA∥CE,AB=CE![]() PA,PA⊥平面ABCD.
PA,PA⊥平面ABCD.
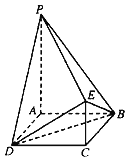
(1)证明:PE⊥平面DBE;
(2)求二面角B﹣PD﹣E的正弦值的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年郑开国际马拉松比赛,于2019年3月31日在郑州、开封举行.某学校本着“我运动,我快乐,我锻炼,我提高”精神,积极组织学生参加比赛及相关活动,为了了解学生的参与情况,从全校学生中随机抽取了150名学生,对是否参与的情况进行了问卷调查,统计数据如下:
会参与 | 不会参与 | |
男生 | 60 | 40 |
女生 | 20 | 30 |
(1)根据上表说明,能否有97.5%的把握认为参与马拉松赛事与性别有关?
(2)现从参与问卷调查且参与赛事的学生中,采用按性别分层抽样的方法选取8人参加2019年马拉松比赛志愿者宣传活动,
①求男、女学生各选取多少人;
②若从这8人中随机选取2人到校广播站开展2019年赛事宣传介绍,求恰好选到2名男生的概率.
附:参考公式:![]() ,其中
,其中![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com