
【题目】设函数![]() 由方程
由方程![]() 确定,对于函数
确定,对于函数![]() 给出下列命题:
给出下列命题:
①存在![]() ,
,![]() ,使得
,使得![]() 成立;
成立;
②![]() ,
,![]() ,使得
,使得![]() 且
且![]() 同时成立;
同时成立;
③对于任意![]() ,
,![]() 恒成立;
恒成立;
④对任意![]() ,
,![]() ,
,![]() ;都有
;都有![]() 恒成立.
恒成立.
其中正确的命题共有( )
A.1个B.2个C.3个D.4个
【答案】A
【解析】
将方程![]() 的绝对值符号去掉,画出函数
的绝对值符号去掉,画出函数![]() 的图象,对命题逐一判断,得:
的图象,对命题逐一判断,得:
对①,函数在![]() 上递减,故①错误;
上递减,故①错误;
对②,即![]() ,
,![]() 均在图象上,讨论点
均在图象上,讨论点![]() 分别在第一、二、四象限代入方程,看是否有实数解;
分别在第一、二、四象限代入方程,看是否有实数解;
对③,![]() 恒成立,即
恒成立,即![]() 恒成立,由图
恒成立,由图![]() 的图象总在
的图象总在![]() 图象的上方,故③正确;
图象的上方,故③正确;
对④,可通过举出反例确定④错误.
由方程![]() 知,
知,
当![]() 且
且![]() 时,方程为
时,方程为![]() ;
;
当![]() 且
且![]() 时,方程为
时,方程为![]() ,不成立;
,不成立;
当![]() 且
且![]() 时,方程为
时,方程为![]() ;
;
当![]() 且
且![]() 时,方程为
时,方程为![]() ,不成立;
,不成立;
作出函数![]() 的图象如图所示,
的图象如图所示,

对于①,![]() 是定义域R上的单调减函数,
是定义域R上的单调减函数,
则对任意![]() ,都有
,都有![]() 恒成立,①错误;
恒成立,①错误;
对于②,假设点![]() 在第一象限,则点
在第一象限,则点![]() 也在第一象限,
也在第一象限,
所以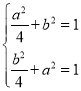 ,该方程组没有实数解,所以该情况不可能;
,该方程组没有实数解,所以该情况不可能;
假设点![]() 在第四象限,则点
在第四象限,则点![]() 在第二象限,
在第二象限,
所以 ,该方程组没有实数解,所以该种情况不可能;
,该方程组没有实数解,所以该种情况不可能;
同理点![]() 在第二象限,则点
在第二象限,则点![]() 在第四象限,也不可能.
在第四象限,也不可能.
故该命题是假命题.
对于③,由图形知,对于任意![]() ,有
,有![]()
即![]() 恒成立,③正确;
恒成立,③正确;
对于④,不妨令![]() ,
,
则![]() 为
为![]() ,
,
又由题![]()
![]() ,则
,则![]()
![]()
![]() ,
,
即![]() 不恒成立,所以④错误.
不恒成立,所以④错误.
综上知,正确的命题序号是③.
故选:A


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,E是棱AB的中点,动点F是侧面ACC1A1(包括边界)上一点,若EF//平面BCC1B1,则动点F的轨迹是( )
A.线段B.圆弧
C.椭圆的一部分D.抛物线的一部分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解运动健身减肥的效果,某健身房调查了20名肥胖者,健身之前他们的体重(单位:![]() )情况如柱形图1所示,经过四个月的健身后,他们的体重情况如柱形图2所示.对比健身前后,关于这20名肥胖者,下面结论正确的是( )
)情况如柱形图1所示,经过四个月的健身后,他们的体重情况如柱形图2所示.对比健身前后,关于这20名肥胖者,下面结论正确的是( )
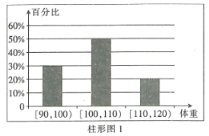
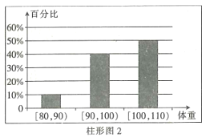
A.他们健身后,体重在区间![]() 内的人数增加了2个
内的人数增加了2个
B.他们健身后,体重在区间![]() 内的人数没有改变
内的人数没有改变
C.因为体重在![]() 内所占比例没有发生变化,所以说明健身对体重没有任何影响
内所占比例没有发生变化,所以说明健身对体重没有任何影响
D.他们健身后,原来体重在区间![]() 内的肥胖者体重都有减少
内的肥胖者体重都有减少
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,M,N,P分别是C1D1,BC,A1D1的中点,有下列四个结论:
①AP与CM是异面直线;②AP,CM,DD1相交于一点;③MN∥BD1;
④MN∥平面BB1D1D.
其中所有正确结论的编号是( )

A.①④B.②④C.①④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】厂家在产品出厂前,需对产品做检验,第一次检测厂家的每件产品合格的概率为![]() ,如果合格,则可以出厂;如果不合格,则进行技术处理,处理后进行第二次检测.每件产品的合格率为
,如果合格,则可以出厂;如果不合格,则进行技术处理,处理后进行第二次检测.每件产品的合格率为![]() ,如果合格,则可以出厂,不合格则当废品回收.
,如果合格,则可以出厂,不合格则当废品回收.
![]() 求某件产品能出厂的概率;
求某件产品能出厂的概率;
![]() 若该产品的生产成本为
若该产品的生产成本为![]() 元/件,出厂价格为
元/件,出厂价格为![]() 元/件,每次检测费为
元/件,每次检测费为![]() 元/件,技术处理每次
元/件,技术处理每次![]() 元/件,回收获利
元/件,回收获利![]() 元/件.假如每件产品是否合格相互独立,记
元/件.假如每件产品是否合格相互独立,记![]() 为任意一件产品所获得的利润,求随机变量
为任意一件产品所获得的利润,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方形ABCD和矩形ACEF中,AB=![]() ,CE=1,CE⊥平面ABCD.
,CE=1,CE⊥平面ABCD.
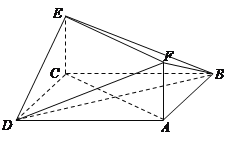
(1)求异面直线DF与BE所成角的余弦值;
(2)求二面角A-DF-B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着全球石油资源紧张、大气污染日益严重和电池技术的提高,电动汽车已被世界公认为21世纪汽车工业改造和发展的主要方向.为了降低对大气的污染和能源的消耗,某品牌汽车制造商研发了两款电动汽车车型![]() 和车型
和车型![]() ,并在黄金周期间同时投放市场.为了了解这两款车型在黄金周的销售情况,制造商随机调查了5家汽车
,并在黄金周期间同时投放市场.为了了解这两款车型在黄金周的销售情况,制造商随机调查了5家汽车![]() 店的销量(单位:台),得到下表:
店的销量(单位:台),得到下表:
| 甲 | 乙 | 丙 | 丁 | 戊 |
车型 | 6 | 6 | 13 | 8 | 11 |
车型 | 12 | 9 | 13 | 6 | 4 |
(1)若从甲、乙两家![]() 店销售出的电动汽车中分别各自随机抽取1台电动汽车作满意度调查,求抽取的2台电动汽车中至少有1台是车型
店销售出的电动汽车中分别各自随机抽取1台电动汽车作满意度调查,求抽取的2台电动汽车中至少有1台是车型![]() 的概率;
的概率;
(2)现从这5家汽车![]() 店中任选3家举行促销活动,用
店中任选3家举行促销活动,用![]() 表示其中车型
表示其中车型![]() 销量超过车型
销量超过车型![]() 销量的
销量的![]() 店的个数,求随机变量
店的个数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com