
1、证明两角差的余弦公式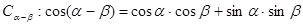 ;
;
2、由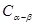 推导两角和的余弦公式
推导两角和的余弦公式 .
.
3、已知△ABC的面积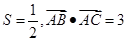 ,且
,且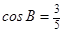 ,求
,求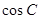 .
.
【解析】本试题主要是考查了利用三角函数总两角和差的三角关系式证明。并能,结合向量的知识进行求解三角形问题的综合运用。
科目:高中数学 来源: 题型:
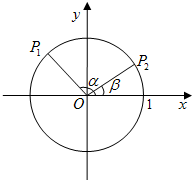 (1)如图,已知α、β是坐标平面内的任意两个角,且0≤α-β≤π,证明两角差的余弦公式:cos(α-β)=cosαcosβ+sinαsinβ;
(1)如图,已知α、β是坐标平面内的任意两个角,且0≤α-β≤π,证明两角差的余弦公式:cos(α-β)=cosαcosβ+sinαsinβ;| π |
| 2 |
| π |
| 2 |
| 1 |
| 3 |
| 7 |
| 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2015届江苏省沭阳县高一下学期期中调研测试数学试卷(解析版) 题型:解答题
(1)如图,已知 是坐标平面内的任意两个角,且
是坐标平面内的任意两个角,且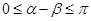 ,证明两角差的余弦公式:
,证明两角差的余弦公式: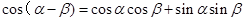 ;
;
(2)已知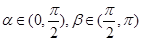 ,且
,且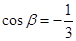 ,
,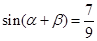 ,求
,求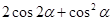 的值.
的值.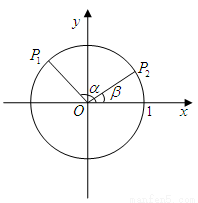
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:陕西省期末题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com