
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)函数![]() 的图象能否与
的图象能否与![]() 轴相切?若能,求出实数
轴相切?若能,求出实数![]() ,若不能,请说明理由;
,若不能,请说明理由;
(2)讨论函数![]() 的单调性.
的单调性.
【答案】(1)见解析;(2)见解析.
【解析】分析:第一问首先对函数求导,之后设出切点坐标,应用切线的斜率等于零以及对应点处的函数值等于零,得到方程组无解,说明没有满足条件的点,从而得到结论;对于第二问,求出函数的导函数,结合其导数的符号,来确定函数在相应区间上的单调性.
详解:(1)由于![]() .
.
假设函数![]() 的图象与
的图象与![]() 轴相切于点
轴相切于点![]() ,
,
则有![]() ,即
,即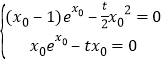 .
.
显然![]() ,将
,将![]() 代入方程
代入方程![]() 中,
中,
得![]() .显然此方程无解.
.显然此方程无解.
故无论![]() 取何值,函数
取何值,函数![]() 的图象都不能与
的图象都不能与![]() 轴相切.
轴相切.
(2)由于![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,![]() 递增,
递增,
当![]() 时,
时,![]() ,
,![]() 递减;
递减;
当![]() 时,由
时,由![]() 得
得![]() 或
或![]() ,
,
①当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 递增,
递增,
当![]() 时,
时,![]() ,
,![]() 递减,
递减,
当![]() ,
,![]() ,
,![]() 递增;
递增;
②当![]() 时,
时,![]() ,
,![]() 递增;
递增;
③当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 递增,
递增,
当![]() 时,
时,![]() ,
,![]() 递减,
递减,
当![]() 时,
时,![]() ,
,![]() 递增.
递增.
综上,当![]() 时,
时,![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数;
上是增函数;
当![]() 时,
时,![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数;
上是减函数;
当![]() 时,
时,![]() 在
在![]() 上是增函数;
上是增函数;
当![]() 时,
时,![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数.
上是减函数.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
【题目】定义新运算:当m≥n时,mn=m;当m<n时,mn=n.设函数f(x)=[(2x2)﹣(1log2x)]2x,则f(x)在(0,2)上值域为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小赵和小王约定在早上![]() 至
至![]() 之间到某公交站搭乘公交车去上学,已知在这段时间内,共有
之间到某公交站搭乘公交车去上学,已知在这段时间内,共有![]() 班公交车到达该站,到站的时间分别为
班公交车到达该站,到站的时间分别为![]() ,
,![]() ,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为__________.
,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最大值与最小值之和为a2+a+1(a>1).
的最大值与最小值之和为a2+a+1(a>1).
(1)求a的值;
(2)判断函数g(x)=f(x)-3在[1,2]的零点的个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆的短轴端点与双曲线
,椭圆的短轴端点与双曲线![]() 的焦点重合,过点
的焦点重合,过点![]() 且不垂直于
且不垂直于![]() 轴的直线
轴的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】写出下列命题的否定,并判断真假:
(1)不论![]() 取何实数,方程
取何实数,方程![]() 必有实数根;
必有实数根;
(2)所有末位数字是0或5的整数都能被5整除;
(3)某些梯形的对角线互相平分;
(4)被8整除的数能被4整除.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校欲在甲、乙两店采购某款投影仪,该投影仪原价为每台2000元,甲店用如下方法促销:买一台单价为1950元,买二台单价为1900元,每多买一台,则所买各台单价均再减50元,但最低不能低于1200元;乙店一律按原售价的80%促销,学校需要购买![]() 台投影仪,若在甲店购买费用为
台投影仪,若在甲店购买费用为![]() 元,若在乙店购买费用记为
元,若在乙店购买费用记为![]() .
.
(1)分别求出![]() 和
和![]() 的解析式;
的解析式;
(2)当购买![]() 台时,在哪家店买更省钱?
台时,在哪家店买更省钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(x,y)在不等式组 表示的平面区域内运动,则z=x-y的取值范围是( )
表示的平面区域内运动,则z=x-y的取值范围是( )
A. [-2,-1] B. [-2,1] C. [-1,2] D. [1,2]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com