
分析 (1)首先,化简函数解析式,借助于辅助角公式进行处理;
(2)结合(1)和三角函数的单调性进行求解.
解答 解:(1)∵f(x)=sin(2x+$\frac{π}{3}$)+sin(2x-$\frac{π}{3}$)+$\sqrt{3}$cos2x.
=sin2xcos$\frac{π}{3}$+cos2xsin$\frac{π}{3}$+sin2xcos$\frac{π}{3}$-cos2xsin$\frac{π}{3}$+$\sqrt{3}$cos2x
=sin2x+$\sqrt{3}$cos2x
=2sin(2x+$\frac{π}{3}$),
∴f(x)=2sin(2x+$\frac{π}{3}$),
∴f($\frac{π}{2}$)=2sin(2×$\frac{π}{2}$+$\frac{π}{3}$)
=2(-sin$\frac{π}{3}$)=-$\sqrt{3}$,
(2)∵-$\frac{π}{2}$+2kπ≤2x+$\frac{π}{3}$≤$\frac{π}{2}$+2kπ,k∈Z,
∴-$\frac{5π}{6}$+2kπ≤2x≤$\frac{π}{6}$+2kπ,
∴-$\frac{5π}{12}$+kπ≤x≤$\frac{π}{12}$+kπ,
∴f(x)的单调增区间[-$\frac{5π}{12}$+kπ,$\frac{π}{12}$+kπ](k∈Z).
点评 本题重点考查了二倍角公式、三角恒等变换公式、三角函数的单调性等知识,属于中档题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{5}{6}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{a}{3}$ | B. | $\frac{a}{4}$ | C. | $\frac{a}{5}$ | D. | $\frac{a}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
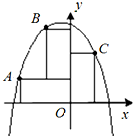 如图,在坐标平面上,沿着两条坐标轴摆着三个相同的长方形,其长、宽分别为4、2,则通过A,B,C三点的拋物线对应的函数关系式是y=-$\frac{5}{12}$x2-$\frac{1}{2}$x+$\frac{20}{3}$.
如图,在坐标平面上,沿着两条坐标轴摆着三个相同的长方形,其长、宽分别为4、2,则通过A,B,C三点的拋物线对应的函数关系式是y=-$\frac{5}{12}$x2-$\frac{1}{2}$x+$\frac{20}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com