
【题目】已知f(x)=ax2+x﹣a.a∈R
(1)若不等式f(x)<b的解集为(﹣∞,﹣1)∪(3,+∞),求a,b的值;
(2)若a<0,解不等式f(x)>1.
【答案】
(1)解:由题意可得方程ax2+x﹣a﹣b=0的两根分别为﹣1、3,且a<0 …(1分)
∴  解得
解得 
(2)解:若a<0,不等式为ax2+x﹣(a+1)>0,即 ![]()
∵ ![]() .
.
∴当 ![]() 时,
时, ![]() ,不等式的解集为
,不等式的解集为 ![]() ;
;
当 ![]() 时,
时, ![]() ,不等式的解集为; …(10分)
,不等式的解集为; …(10分)
当 ![]() 时,
时, ![]() ,不等式的解集为
,不等式的解集为 ![]()
【解析】(1)由题意可得方程ax2+x﹣a﹣b=0的两根分别为﹣1、3,且a<0,利用韦达定理,可得a,b的值;(2)若a<0,等式为ax2+x﹣(a+1)>0,即 ![]() ,分类讨论,可得不同情况下不等式的解集.
,分类讨论,可得不同情况下不等式的解集.
【考点精析】掌握二次函数的性质是解答本题的根本,需要知道当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.


科目:高中数学 来源: 题型:
【题目】如图,二面角α﹣l﹣β的大小为60°,A∈β,C∈α,且AB、CD都垂直于棱l,分别交棱l于B、D.已知BD=1,AB=2,CD=3,则AC= . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面使用类比推理正确的是( )
A.直线a∥b,b∥c,则a∥c,类推出:向量 ![]() ,
, ![]() ,则
,则 ![]()
B.同一平面内,直线a,b,c,若a⊥c,b⊥c,则a∥b.类推出:空间中,直线a,b,c,若a⊥c,b⊥c,则a∥b
C.实数a,b,若方程x2+ax+b=0有实数根,则a2≥4b.类推出:复数a,b,若方程x2+ax+b=0有实数根,则a2≥4b
D.以点(0,0)为圆心,r为半径的圆的方程为x2+y2=r2 . 类推出:以点(0,0,0)为球心,r为半径的球的方程为x2+y2+z2=r2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长时间用手机上网严重影响着学生的身体健康,某校为了解A、B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字). 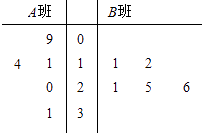
(Ⅰ)分别求出图中所给两组样本数据的平均值,并据此估计,哪个班的学生平均上网时间较长;
(Ⅱ)从A班的样本数据中随机抽取一个不超过19的数据记为a,从B班的样本数据中随机抽取一个不超过21的数据记为b,求a>b的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=2|x﹣4|﹣logax+2无零点,则实数a的取值范围为;
若函数f(x)=|2x﹣2|﹣b有两个零点,则实数b的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com