
【题目】某大型歌手选秀活动,过程分为初赛、复赛和决赛.经初赛进入复赛的40名选手被平均分成甲、乙两个班,由组委会聘请两位导师各负责一个班进行声乐培训.下图是根据这40名选手参加复赛时获得的100名大众评审的支持票数制成的茎叶图.赛制规定:参加复赛的40名选手中,获得的支持票数不低于85票的可进入决赛,其中票数不低于95票的选手在决赛时拥有“优先挑战权”.
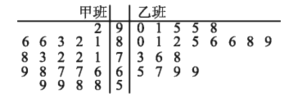
(1)从进入决赛的选手中随机抽出2名,X表示其中拥有“优先挑战权”的人数,求X的分布列和数学期望;
(2)请填写下面的![]() 列联表,并判断能否在犯错误的概率不超过0.025的前提下认为进入决赛与选择的导师有关?
列联表,并判断能否在犯错误的概率不超过0.025的前提下认为进入决赛与选择的导师有关?
甲班 | 乙班 | 合计 | |
进入决赛 | |||
未进入决赛 | |||
合计 |
下面的临界值表仅供参考:
P( | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: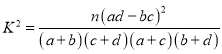 ,其中
,其中![]() )
)
【答案】(1)分布列见解析,![]() ;(2)列联表见解析,在犯错误的概率不超过0.025的前提下可以认为进入决赛与选择的导师有关.
;(2)列联表见解析,在犯错误的概率不超过0.025的前提下可以认为进入决赛与选择的导师有关.
【解析】
(1)由题中茎叶图可知, X的可能取值为0,1,2,再求出对应的概率,即得X的分布列和数学期望;(2)由茎叶图得![]() 列联表,求出
列联表,求出![]() 即得解.
即得解.
(1)由题中茎叶图可知,进入决赛的选手共13名,其中拥有“优先挑战权”的选手共3名.
根据题意,X的可能取值为0,1,2.
![]() ,
,![]() ,
,![]() .
.
X的分布列如下:
X | 0 | 1 | 2 |
P |
|
|
|
![]() .
.
(2)由茎叶图可得![]() 列联表如下:
列联表如下:
甲班 | 乙班 | 合计 | |
进入决赛 | 3 | 10 | 13 |
未进入决赛 | 17 | 10 | 27 |
合计 | 20 | 20 | 40 |
![]() ,
,
因此在犯错误的概率不超过0.025的前提下可以认为进入决赛与选择的导师有关.


科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且B是A,C的等差中项.
(1)若![]() ,求边c的值;
,求边c的值;
(2)设t=sinAsinC,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的导函数为
的导函数为![]() ,且对任意的实数x都有
,且对任意的实数x都有![]() (e是自然对数的底数),且
(e是自然对数的底数),且![]() ,若关于x的不等式
,若关于x的不等式![]() 的解集中恰有两个整数,则实数m的取值范围是( )
的解集中恰有两个整数,则实数m的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A1,A2,…,An,…B1,B2,…,Bn,…均在抛物线x=y2上,线段AnBn与x轴的交点为Hn.将△OA1B1,△H1A2B2,…,△HnAn+1Bn+1,…的面积分别记为S1,S2,…,Sn+1,….已知上述三角形均为等腰直角三角形,且它们的顶角分别为O,H1,…,Hn,….
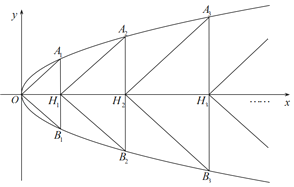
(1)求S1和S2的值;
(2)证明:n≤sn≤n2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的函数
上的函数![]() 满足
满足![]() ,且
,且![]() ,则下列说法正确的有( )
,则下列说法正确的有( )
(1)若函数![]() ,则函数
,则函数![]() 是奇函数;
是奇函数;
(2)![]() ;
;
(3)设函数![]() ,则函数
,则函数![]() 的图象经过点
的图象经过点![]() ;
;
(4)设![]() ,若数列
,若数列![]() 是等比数列,则
是等比数列,则![]() .
.
A.(2)(3)(4)B.(1)(3)(4)C.(1)(3)D.(1)(2)(3)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义函数f(x)=(1﹣x2)(x2+bx+c).
(1)如果f(x)的图象关于x=2对称,求2b+c的值;
(2)若x∈[﹣1,1],记|f(x)|的最大值为M(b,c),当b、c变化时,求M(b,c)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,恰好又是双曲线
的焦点,恰好又是双曲线![]() 的右焦点,双曲线
的右焦点,双曲线![]() 过点
过点![]() ,且其离心率为
,且其离心率为![]() .
.
(1)求抛物线![]() 和双曲线
和双曲线![]() 的标准方程;
的标准方程;
(2)已知直线![]() 过点
过点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() ,
,![]() 两点,以
两点,以![]() 为直径作圆
为直径作圆![]() ,设圆
,设圆![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com