练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设长方体ABCD-A1B1C1D1中，AB=1，AA1=2
    		3
    ，AD=2，M和N分别为AA1和BB1的中点，若θ为直线CM与D1N所成的角，则θ等于（　　）
    分析：建立空间直角坐标系，利用向量夹角求解．
    解答：解：如图建立空间直角坐标系，
    则D1（0，0，0），M（2，0，
    		3
    ），N（2，1，
    		3
    ），C（0，1，2
    		3
    ），
    D1N
    =（2，1，
    		3
    ），
    CM
    =（2，-1，-
    		3
    ），
    ∵
    D1N
    •
    CM
    =2×2-1×1-
    		3
    ×
    		3
    =0，
    ∴
    D1N
    ⊥
    CM
    ，
    所以直线CM与D1N所成的角为90°，即θ等于90°，
    故选D．
    点评：本题考查异面直线所成角的求解，考查空间向量的运算，属中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

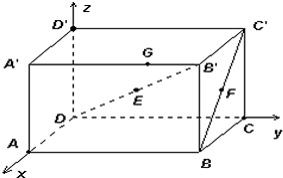    精英家教网如图，长方体ABCD-A'B'C'D'中，|AD|=3，|AB|=5，|AA'|=3，设E为DB'的中点，F为BC'的中点，在给定的空间直角坐标系D-xyz下，试写出A，B，C，D，A'，B'，C'，D'，E，F各点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体，圆柱也叫长方体的外接圆柱．设长方体ABCD-A1B1C1D1的长、宽、高分别为a，b，c（其中a＞b＞c），那么该长方体的外接圆柱侧面积的最大值等于（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若多面体的各个顶点都在同一球面上，则称这个多面体内接于球．如图，设长方体ABCD-A1B1C1D1内接于球O，且AB=BC=2，AA1=2
    		2
    ，则A、B两点之间的球面距离为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知长方体ABCD—A′B′C′D′，设=a，=b，=c，E、F分别为AA′、C′D′中点，则可用a、b、c表示为___________________.

    查看答案和解析>>

    同步练习册答案