已知函数f(x)=(x2-ax+1)eax,其中a∈R,x∈R若函数.y=f(x)在点(1,f(1))处的切线与X轴平行.
(I)求实数a的值;
(II)求函数y=f(x)的单调区间;
(III)当a>0时,设g(x)=lnf(x),当,x∈(1,+∞)时,函数g(x)图象上是否存在两点,使得过此两点处的切线互相垂直?证明你的结论.
【答案】
分析:(I)先由所给函数的表达式,求导数fˊ(x),再根据导数的几何意义求出切线的斜率,最后由平行直线的斜率相等方程求a的值即可;
(II)对参数a进行分类,令导数fˊ(x)>0,解不等式即可求出f(x)的单调性;
(III)先由(I)得出a的值,然后假设存在两点使得过此两点处的切线互相垂直,求出函数的导数,再根据k
1•k
2=-1,列出关于x
1、x
2的不等式,推出矛盾就可得出结论.
解答:解:f'(x)=e
ax[ax
2-(a
2-2)x]
(1)因为f(x)在点(1,f(1))处的切线与X轴平行.
f'(1)=0,即a-a
2+2=0
解得a=-1或2
(2)由f'(x)=e
ax[ax
2-(a
2-2)x]得
①a=2时,f'(x)=e
2x(2x
2-2x)
由f'(x)>0得
x>1或x<0
∴函数f(x)的单调递增区间是(-∞,0)和(1,+∞),单调递减区间是(0,1)
②a=-1时,令f'(x)>0得0<x<1
∴函数f(x)的单调递增区间是(0,1),单调递减区间是 (-∞,0)和(1,+∞)
(III)当a>0时,由(1)知a=2
∵g(x)=lnf(x)=ln(x
2-2x+1)+2x
假设存在两点A、B,使得过此两点处的切线互相垂直,则由
g'(x)=

知斜率k
1=g'(x
1)=
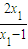
k
2=g'(x
2)=

且k
1•k
2=-1∵x∈(1,+∞)
∴x1-1>0,x2-1>0
∴

,因此上式矛盾!故假设不成立.
∴函数上不存在两点A、B,使得过此两点处的切线互相垂直.
点评:本题主要考查利用导数研究曲线上某点切线方程、两条直线平行的判定等基础知识,会利用导数研究函数的单调区间,考查推理能力.


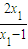 k2=g'(x2)=
k2=g'(x2)=
 ,因此上式矛盾!故假设不成立.
,因此上式矛盾!故假设不成立.

 名校课堂系列答案
名校课堂系列答案