
在(a-2b)![]() 的展开式中,
的展开式中,
(1) 若n=10,求展开式的倒数第四项(要求将系数计算到具体数值)
(2) 若展开式中二项式系数不超过6的项恰好有5项,求n的值;
(3) 若展开式中系数不超过6的项恰好有五项,求n的值。
解析:(1)(a-2b)![]() 展开式的通项公式(即第r+1项)是:
展开式的通项公式(即第r+1项)是:![]()
n=10时,展开式共有11项,其倒数第四项即第八项。
![]()
(2)展开式中二项式系数不超过6的项恰好有5项,
一方面说明![]() ,5项存在。
,5项存在。
另一方面说明展开式的第二项的二项式系数也不超过6,即![]()
当n=4时,各项的二项式系数分别是1,4,6,4,1,恰好有5项二项式系数不超过6。
当n=5,各项的二项式系数分别是1,5,10,10,5,1,没有5项二项式系数不超过6.
当n=6,各项的二项式系数分别是1,6,15,20,15,6,1,没有5项的二项式系数不超过6.
所以,所求n的值等于4.
(3) 展开式第r+1项的系数是![]()
展开式种的第一项系数等于1,不超过6;
要展开式有5项,![]()
展开式种所有偶数项的习俗均为负,故偶数项不能超过4项,即![]()
当n=4时,各项的习俗分别是1,-8,24,-32,16,没有5项系数不超过6.
类似地,n=5,n=6时,展开式种都没有5项系数不超过6.
当n=7时,第1,2,4,6,8项的习俗不超过6.
当n=8时,第1,2,4,6,8项的习俗不超过6.
所以,所求n的值等于7或者8.、


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
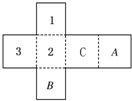 如图是一个正方体盒子的平面展开图,在其中的两个正方形内标有数字1、2、3,要在其余正方形内分别填上-1、-2、-3,使得按虚线折成正方体后,相对面上的两数互为相反数,则A处应填( )
如图是一个正方体盒子的平面展开图,在其中的两个正方形内标有数字1、2、3,要在其余正方形内分别填上-1、-2、-3,使得按虚线折成正方体后,相对面上的两数互为相反数,则A处应填( )查看答案和解析>>
科目:高中数学 来源: 题型:单选题
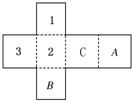 如图是一个正方体盒子的平面展开图,在其中的两个正方形内标有数字1、2、3,要在其余正方形内分别填上-1、-2、-3,使得按虚线折成正方体后,相对面上的两数互为相反数,则A处应填
如图是一个正方体盒子的平面展开图,在其中的两个正方形内标有数字1、2、3,要在其余正方形内分别填上-1、-2、-3,使得按虚线折成正方体后,相对面上的两数互为相反数,则A处应填查看答案和解析>>
科目:高中数学 来源:2012-2013学年贵州省安顺学院附中高二(上)期中数学试卷(理科)(解析版) 题型:选择题
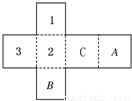
查看答案和解析>>
科目:高中数学 来源:2012-2013学年贵州省安顺学院附中高二(上)期中数学试卷(理科)(解析版) 题型:选择题
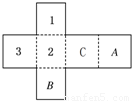
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com