练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

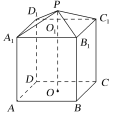
    【题目】现需要设计一个仓库，它由上下两部分组成，上部的形状是正四棱锥P－A1B1C1D1，下部的形状是正四棱柱ABCD－A1B1C1D1(如图所示)，并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍，若AB＝6 m，PO1＝2 m，则仓库的容积是多少？

    【答案】

    【解析】

    分别计算四棱锥和四棱柱的体积，相加即得．

    由PO1＝2 m，知O1O＝4PO1＝8 m.因为A1B1＝AB＝6 m，所以正四棱锥P－A1B1C1D1的体积V锥＝··PO1＝×62×2＝24(m3)；

    正四棱柱ABCD－A1B1C1D1的体积

    V柱＝AB2·O1O＝62×8＝288(m3)，

    所以仓库的容积V＝V锥＋V柱＝24＋288＝312(m3).

    故仓库的容积是312 m3.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）讨论的单调性；

    （2）若在区间上有两个零点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从2名男生和2名女生中任意选择两人在星期六、星期日参加某公益活动,每天一人,则星期六安排一名男生、星期日安排一名女生的概率为(　　)

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从数字1，2，3，4，5中，随机抽取3个数字（允许重复）组成一个三位数，其各位数字之和等于9的概率为 （ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知Sn为数列{an}的前n项和，且Sn+2＝2an，n∈N*.

    （1）求数列{an}的通项公式；

    （2）令bn，设数列{bn}的前项和为Tn，若Tn，求n的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知某单位有甲、乙、丙三个部门，从员工中抽取7人，进行睡眠时间的调查．若抽出的7人中有4人睡眠不足，3人睡眠充足，现从这7人中随机抽取3人做进一步的身体检查．

    （1）用X表示抽取的3人中睡眠不足的员工人数，求随机变量X的分布列与数学期望；

    （2）设A为事件“抽取的3人中，既有睡眠充足的员工，也有睡眠不足的员工”，求事件A发生的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】去年，相关部门对某城市“五朵金花”之一的某景区在“十一”黄金周中每天的游客人数作了统计，其频率分布如下表所示：

    时间

    10月1日

    10月2日

    10月3日

    10月4日

    10月5日

    10月6日

    10月7日

    频率

    0.05

    0.08

    0.09

    0.13

    0.30

    0.15

    0.20

    已知10月1日这天该景区的营业额约为8万元，假定这七天每天游客人均消费相同，则这个黄金周该景区游客人数最多的那一天的营业额约为______万元.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知下列命题：

    ①在线性回归模型中，相关指数越接近于1，表示回归效果越好；

    ②两个变量相关性越强，则相关系数r就越接近于1；

    ③在回归直线方程中，当解释变量每增加一个单位时，预报变量平均减少0.5个单位；

    ④两个模型中残差平方和越小的模型拟合的效果越好.

    ⑤回归直线恒过样本点的中心，且至少过一个样本点；

    ⑥若的观测值满足≥6.635，我们有99%的把握认为吸烟与患肺病有关系，那么在100个吸烟的人中必有99人患有肺病；

    ⑦从统计量中得知有95%的把握认为吸烟与患肺病有关系，是指有5%的可能性使得推断出现错误． 其中正确命题的序号是__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设是大于1的自然数，找出所有自然数，使得对于存在互质的自然数、，满足.

    查看答案和解析>>

    同步练习册答案