
【题目】如图,设O是平行四边形ABCD的两条对角线AC,BD的交点,下列向量组:
① ![]() 与
与 ![]() ;②
;② ![]() 与
与 ![]() ;
;
③ ![]() 与
与 ![]() ;④
;④ ![]() 与
与 ![]() .
.
其中可作为这个平行四边形所在平面的一组基底的是( ).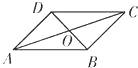
A.①②
B.③④
C.①③
D.①④
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线C:x2=4y的焦点为F,过点F且斜率为1的直线与抛物线相交于M、N两点,设直线l是抛物线C的切线,且l∥MN,P为l上一点,则 ![]() 的最小值为 .
的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答题。
(1)解方程4x﹣2x﹣2=0.
(2)求不等式 log2(2x+3)>log2(5x﹣6);
(3)求函数y=( ![]() )
) ![]() ,x∈[0,5)的值域.
,x∈[0,5)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=3|x|+log3|x|.
(1)判断函数的奇偶性,并加以证明;
(2)说明函数f(x)在(0,+∞)上的单调性,并利用单调性定义证明;
(3)若 f(2a)<28,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=kax﹣a﹣x(a>0且a≠1,k∈R),f(x)是定义域为R的奇函数.
(1)求k的值
(2)已知f(1)= ![]() ,函数g(x)=a2x+a﹣2x﹣2f(x),x∈[0,1],求g(x)的值域;
,函数g(x)=a2x+a﹣2x﹣2f(x),x∈[0,1],求g(x)的值域;
(3)在第(2)问的条件下,试问是否存在正整数λ,使得f(2x)≥λf(x)对任意x∈[﹣ ![]() ,
, ![]() ]恒成立?若存在,请求出所有的正整数λ;若不存在,请说明理由.
]恒成立?若存在,请求出所有的正整数λ;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度为( ) 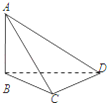
A.10 ![]() m
m
B.20m
C.20 ![]() m
m
D.40m
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个匀速旋转的摩天轮每12分钟转一周,最低点距地面2米,最高点距地面18米,P是摩天轮轮周上一定点,从P在最低点时开始计时,则16分钟后P点距地面的高度是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=(a+1)x﹣2+1(a>0)的图象恒过定点A,且点A又在函数 ![]() 的图象上.
的图象上.
(1)求实数a的值;
(2)解不等式f(x)< ![]() ;
;
(3)函数h(x)=|g(x+2)﹣2|的图象与直线y=2b有两个不同的交点时,求b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com