
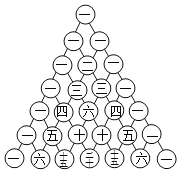
【题目】杨辉三角,又称帕斯卡三角,是二项式系数在三角形中的一种几何排列,在我国南宋数学家杨辉所著的《评解九章算法》(![]() 年)一书中用如图所示的三角形解释二项式乘方展开式的系数规律,现把杨辉三角中的数从上到下,从左到右依次排列,得数列:
年)一书中用如图所示的三角形解释二项式乘方展开式的系数规律,现把杨辉三角中的数从上到下,从左到右依次排列,得数列:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() …….记作数列
…….记作数列![]() ,若数列
,若数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】某城市9年前分别同时开始建设物流城和湿地公园,物流城3年建设完成,建成后若年投入x亿元,该年产生的经济净效益为![]() 亿元;湿地公园4年建设完成,建成后的5年每年投入见散点图.公园建成后若年投入x亿元,该年产生的经济净效益为
亿元;湿地公园4年建设完成,建成后的5年每年投入见散点图.公园建成后若年投入x亿元,该年产生的经济净效益为![]() 亿元.
亿元.

(1)对湿地公园,请在![]() 中选择一个合适模型,求投入额x与投入年份n的回归方程;
中选择一个合适模型,求投入额x与投入年份n的回归方程;
(2)从建设开始的第10年,若对物流城投入0.25亿元,预测这一年物流城和湿地公园哪个产生的年经济净效益高?请说明理由.
参考数据及公式:![]() ,
,![]() ;当
;当![]() 时,
时,![]() ,
,![]() ,回归方程中的
,回归方程中的![]() ;回归方程
;回归方程![]() 斜率与截距
斜率与截距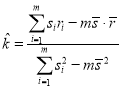 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知曲线![]() (
(![]() 为参数),直线
为参数),直线![]() (
(![]() 为参数,
为参数, ![]() ),直线
),直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程及点
的极坐标方程及点![]() 的极坐标;
的极坐标;
(2)曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于在
交于在![]() ,
,![]() 两点,记
两点,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运动制衣品牌为了成衣尺寸更精准,现选择15名志愿者,对其身高和臂展进行测量(单位:厘米),左图为选取的15名志愿者身高与臂展的折线图,右图为身高与臂展所对应的散点图,并求得其回归方程为![]() ,以下结论中不正确的为
,以下结论中不正确的为


A. 15名志愿者身高的极差小于臂展的极差
B. 15名志愿者身高和臂展成正相关关系,
C. 可估计身高为190厘米的人臂展大约为189.65厘米,
D. 身高相差10厘米的两人臂展都相差11.6厘米,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A是以BC为直径的圆O上异于B,C的动点,P为平面ABC外一点,且平面PBC⊥平面ABC,BC=3,PB=2![]() ,PC
,PC![]() ,则三棱锥P﹣ABC外接球的表面积为______.
,则三棱锥P﹣ABC外接球的表面积为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是指大气中直径小于或等于
是指大气中直径小于或等于![]() 微米的颗粒物,也称为可吸入肺颗粒物.我国
微米的颗粒物,也称为可吸入肺颗粒物.我国![]() 标准采用世卫组织设定的最宽限值,即
标准采用世卫组织设定的最宽限值,即![]() 日均值在35微克/立方米以下空气质量为一级;在35微克/立方米
日均值在35微克/立方米以下空气质量为一级;在35微克/立方米![]() 微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标,某试点城市环保局从该市市区2019年上半年每天的
微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标,某试点城市环保局从该市市区2019年上半年每天的![]() 监测数据中随机的抽取15天的数据作为样本,监测值如下茎叶图所示(十位为茎,个位为叶).
监测数据中随机的抽取15天的数据作为样本,监测值如下茎叶图所示(十位为茎,个位为叶).
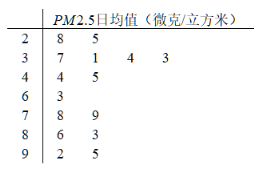
(1)在这15天的![]() 日均监测数据中,求其中位数;
日均监测数据中,求其中位数;
(2)从这15天的数据中任取2天数据,记![]() 表示抽到
表示抽到![]() 监测数据超标的天数,求
监测数据超标的天数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3)以这15天的![]() 日均值来估计该市下一年的空气质量情况,则一年(按365天计算)中平均有多少天的空气质量达到一级或二级.
日均值来估计该市下一年的空气质量情况,则一年(按365天计算)中平均有多少天的空气质量达到一级或二级.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等比数列![]() 中,已知
中,已知![]() 设数列
设数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]()
(1)求数列![]() 通项公式;
通项公式;
(2)证明:数列![]() 是等差数列;
是等差数列;
(3)是否存在等差数列![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ?若存在,求出所有符合题意的等差数列
?若存在,求出所有符合题意的等差数列![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )经过点
)经过点![]() ,且两个焦点
,且两个焦点![]() ,
,![]() 的坐标依次为
的坐标依次为![]() 和
和![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个动点,
上的两个动点,![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,若
,若![]() ,证明:直线
,证明:直线![]() 与以原点为圆心的定圆相切,并写出此定圆的标准方程.
与以原点为圆心的定圆相切,并写出此定圆的标准方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com