练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．为了了解某同学的数学学习情况，对他的6次数学测试成绩（满分100分）进行统计，作出的茎叶图如图所示，则该同学数学成绩的中位数为84．

    分析 根据茎叶图中的数据，计算数据的中位数即可．

    解答 解：根据茎叶图，得到6次数学成绩为：78，83，83，85，90，91，中位数是$\frac{83+85}{2}$=84，
    故答案为：84．

    点评 本题考查了茎叶图的应用问题，解题时应根据茎叶图中的数据进行有关的计算，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    18．已知数列{an}中，a1=3，a2=5，且对于任意的大于2的正整数n，有an=an-1-an-2，则a2015=-5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知定义在R上的奇函数f（x）满足f（x-2）=-f（x），则f（2006）的值为（　　）
    A．2006B．1003C．0D．不确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知函数f（x）=kx+m，当x∈[a1，b1]时，f（x）的值域为[a2，b2]，当x∈[a2，b2]时，f（x）的值域为[a3，b3]，依此类推，一般地，当x∈[an-1，bn-1]时，f（x）的值域为[an，bn]，其中k、m为常数，且a1=0，b1=1．
    （1）若k=1，求数列{an}，{bn}的通项公式；
    （2）若m=2，问是否存在常数k＞0，使得数列{bn}满足$\underset{lim}{n→∞}$bn=4？若存在，求k的值；若不存在，请说明理由；
    （3）若k＜0，设数列{an}，{bn}的前n项和分别为Sn，Tn，求（T1+T2+…+T2014）-（S1+S2+…+S2014）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

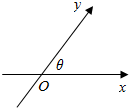    3．如图，数轴x，y的交点为O，夹角为θ，与x轴、y轴正向同向的单位向量分别是$\overrightarrow{e_1}，\overrightarrow{e_2}$．由平面向量基本定理，对于平面内的任一向量$\overrightarrow{OP}$，存在唯一的有序实数对（x，y），使得$\overrightarrow{OP}=x\overrightarrow{e_1}+y\overrightarrow{e_2}$，我们把（x，y）叫做点P在斜坐标系xOy中的坐标（以下各点的坐标都指在斜坐标系xOy中的坐标）．
    （1）若θ=90°，$\overrightarrow{OP}$为单位向量，且$\overrightarrow{OP}$与$\overrightarrow{e_1}$的夹角为120°，求点P的坐标；
    （2）若θ=45°，点P的坐标为$（{1，\sqrt{2}}）$，求向量$\overrightarrow{OP}$与$\overrightarrow{e_1}$的夹角；
    （3）若θ=60°，求过点A（2，1）的直线l的方程，使得原点O到直线l的距离最大．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知数列{an}的首项a1=$\frac{3}{4}$，an+1=$\frac{3{a}_{n}}{2{a}_{n}+1}$，n=1，2，3…
    （1）证明：数列{$\frac{1}{{a}_{n}}$-1}是等比数列；
    （2）是否存在互不相等的正整数m，s，t成等差数列，且am-1，as-1，at-1成等比数列？如果存在，求出所有符合条件的m，s，t，如果不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知集合$A=\left\{{x\left|{\frac{{{x^2}-x-6}}{x+1}≤0}\right.}\right\}$，集合B={x||x+2a|≤a+1，a∈R}．
    （1）求集合A与集合B；
    （2）若A∩B=B，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．圆心在直线2x+y=0上，且与直线x-y+1=0切与点P（2，-1）的圆的标准方程（x-1）2+（y+2）2=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．已知点P为圆C：x2+y2-4x-4y+4=0上的动点，点P到某直线l的最大距离为5，若在直线l上任取一点A作圆C的切线AB，切点为B，则AB的最小值是$\sqrt{5}$．

    查看答案和解析>>

    同步练习册答案